
Question Number 145240 by loveineq last updated on 03/Jul/21
![Let a,b,c ≥ 0 and a^2 +b^2 +c^2 = 3. Prove that (1) Σ_(cyc) a^3 +Σ_(cyc) (a+b)^3 ≤ 27 (2) a^3 +b^3 +(b+c)^3 +(c+a)^3 ≥ (1/2)[c^3 +(a+b)^3 ] (3) For a≥b≥c≥0, a^3 +b^3 +(b+c)^3 +(c+a)^3 ≤ 2[c^3 +(a+b)^3 ]](Q145240.png)
$$\mathrm{Let}\:{a},{b},{c}\:\geqslant\:\mathrm{0}\:\mathrm{and}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \:=\:\mathrm{3}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{cyc}} {\sum}{a}^{\mathrm{3}} +\underset{{cyc}} {\sum}\left({a}+{b}\right)^{\mathrm{3}} \:\leqslant\:\mathrm{27} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\left({b}+{c}\right)^{\mathrm{3}} +\left({c}+{a}\right)^{\mathrm{3}} \:\geqslant\:\frac{\mathrm{1}}{\mathrm{2}}\left[{c}^{\mathrm{3}} +\left({a}+{b}\right)^{\mathrm{3}} \right] \\ $$$$\left(\mathrm{3}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{For}\:{a}\geqslant{b}\geqslant{c}\geqslant\mathrm{0},\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\left({b}+{c}\right)^{\mathrm{3}} +\left({c}+{a}\right)^{\mathrm{3}} \:\leqslant\:\mathrm{2}\left[{c}^{\mathrm{3}} +\left({a}+{b}\right)^{\mathrm{3}} \right] \\ $$
Answered by mitica last updated on 03/Jul/21
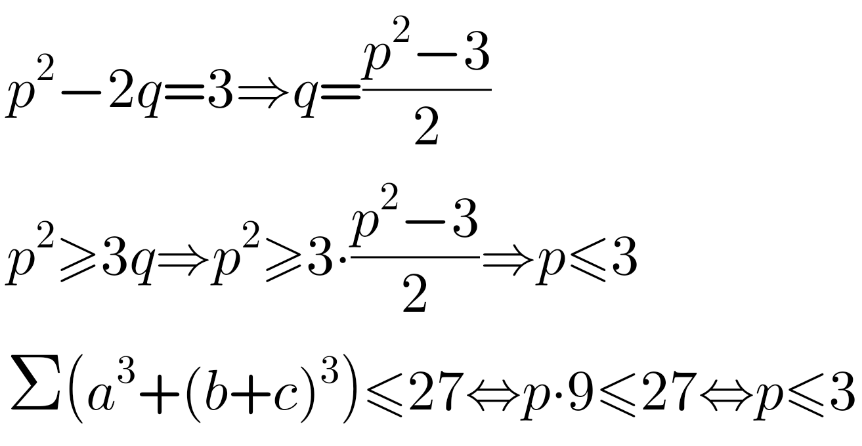
Commented by loveineq last updated on 03/Jul/21
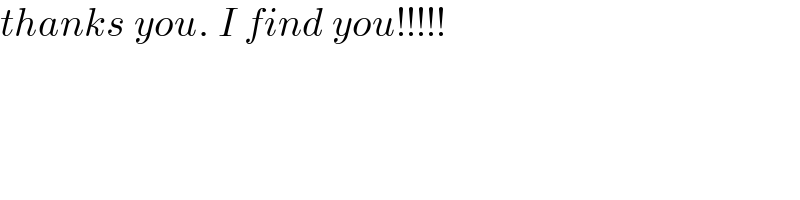
$${thanks}\:{you}.\:{I}\:{find}\:{you}!!!!! \\ $$
