
Question Number 1778 by 112358 last updated on 23/Sep/15
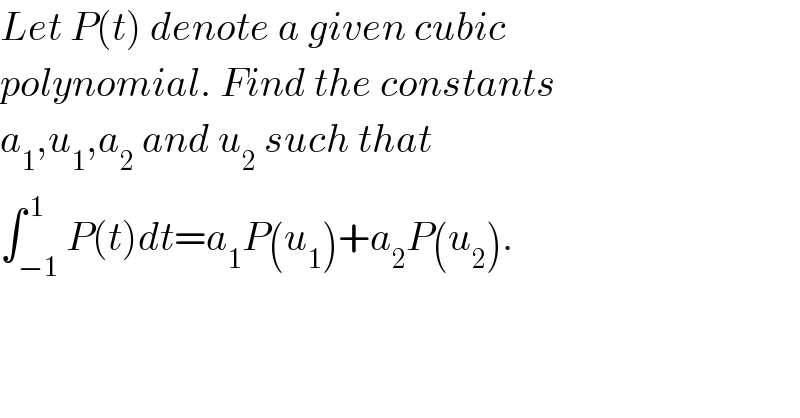
$${Let}\:{P}\left({t}\right)\:{denote}\:{a}\:{given}\:{cubic} \\ $$$${polynomial}.\:{Find}\:{the}\:{constants} \\ $$$${a}_{\mathrm{1}} ,{u}_{\mathrm{1}} ,{a}_{\mathrm{2}} \:{and}\:{u}_{\mathrm{2}} \:{such}\:{that} \\ $$$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} {P}\left({t}\right){dt}={a}_{\mathrm{1}} {P}\left({u}_{\mathrm{1}} \right)+{a}_{\mathrm{2}} {P}\left({u}_{\mathrm{2}} \right). \\ $$
Answered by Rasheed Soomro last updated on 23/Sep/15
![Let P(t)=at^3 +bt^2 +ct+d LHS: ∫P(t)dt=(a/4)t^4 +(b/3)t^3 +(c/2)t^2 +dt+C ∫_(−1) ^( 1) P(t)dt=[(a/4)t^4 +(b/3)t^3 +(c/2)t^2 +dt+C]_(−1) ^1 =[(a/4)+(b/3)+(c/2)+d+C]−[(a/4)−(b/3)+(c/2)−d+C] =((2b)/3)+2d RHS: a_1 P(u_1 )+a_2 P(u_2 ) =a_1 {a(u_1 )^3 +b(u_1 )^2 +c(u_1 )+d}+a_2 {a(u_2 )^3 +b(u_2 )^2 +cu_2 +d} Comparing coefficients of b and d in LHS and RHS (2/3)=a_1 (u_1 )^2 +a_2 (u_2 )^2 and 2=a_1 +a_2 Solving simultaneously 3(u_1 )^2 a_1 +3(u_1 )^2 a_2 =6(u_1 )^2 ............I 3(u_1 )^2 a_1 +3(u_2 )^2 a_2 =2 ............II Subtracting II from I 3{(u_1 )^2 −(u_2 )^2 }a_2 =6(u_1 )^2 −2 a_2 =((6(u_1 )^2 −2)/(3{(u_1 )^2 −(u_2 )^2 })) Similarly, a_1 =((6(u_2 )^2 −2)/(3{(u_2 )^2 −(u_1 )^2 })) I think u_1 and u_2 should be taken as arbitrary constants. Or otherwise if a_1 and a_2 are taken as arbitrary then u_1 and u_2 can be determined.](Q1779.png)
$${Let}\:{P}\left({t}\right)={at}^{\mathrm{3}} +{bt}^{\mathrm{2}} +{ct}+{d} \\ $$$${LHS}: \\ $$$$\:\:\:\:\:\:\int{P}\left({t}\right)\boldsymbol{\mathrm{d}}{t}=\frac{{a}}{\mathrm{4}}{t}^{\mathrm{4}} +\frac{{b}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{{c}}{\mathrm{2}}{t}^{\mathrm{2}} +{dt}+{C} \\ $$$$\:\:\:\:\:\:\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} {P}\left({t}\right)\boldsymbol{\mathrm{d}}{t}=\left[\frac{{a}}{\mathrm{4}}{t}^{\mathrm{4}} +\frac{{b}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{{c}}{\mathrm{2}}{t}^{\mathrm{2}} +{dt}+{C}\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{{a}}{\mathrm{4}}+\frac{{b}}{\mathrm{3}}+\frac{{c}}{\mathrm{2}}+{d}+{C}\right]−\left[\frac{{a}}{\mathrm{4}}−\frac{{b}}{\mathrm{3}}+\frac{{c}}{\mathrm{2}}−{d}+{C}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{b}}{\mathrm{3}}+\mathrm{2}{d} \\ $$$${RHS}: \\ $$$$\:\:\:\:\:\:\:{a}_{\mathrm{1}} {P}\left({u}_{\mathrm{1}} \right)+{a}_{\mathrm{2}} {P}\left({u}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:={a}_{\mathrm{1}} \left\{{a}\left({u}_{\mathrm{1}} \right)^{\mathrm{3}} +{b}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} +{c}\left({u}_{\mathrm{1}} \right)+{d}\right\}+{a}_{\mathrm{2}} \left\{{a}\left({u}_{\mathrm{2}} \right)^{\mathrm{3}} +{b}\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} +{cu}_{\mathrm{2}} +{d}\right\} \\ $$$${Comparing}\:{coefficients}\:{of}\:{b}\:\:{and}\:\:{d}\:{in}\:{LHS}\:\:{and}\:\:{RHS} \\ $$$$\:\:\:\frac{\mathrm{2}}{\mathrm{3}}={a}_{\mathrm{1}} \left({u}_{\mathrm{1}} \right)^{\mathrm{2}} +{a}_{\mathrm{2}} \left({u}_{\mathrm{2}} \right)^{\mathrm{2}} \:\:\:\:{and}\:\:\:\mathrm{2}={a}_{\mathrm{1}} +{a}_{\mathrm{2}} \\ $$$${Solving}\:{simultaneously} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} \:{a}_{\mathrm{1}} +\mathrm{3}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} {a}_{\mathrm{2}} =\mathrm{6}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} \:\:\:\:............{I} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} {a}_{\mathrm{1}} +\mathrm{3}\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} {a}_{\mathrm{2}} =\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:............{II} \\ $$$$\:{Subtracting}\:\:{II}\:\:\:{from}\:\:\:{I} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3}\left\{\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} −\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} \right\}{a}_{\mathrm{2}} =\mathrm{6}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}_{\mathrm{2}} =\frac{\mathrm{6}\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{2}}{\mathrm{3}\left\{\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} −\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} \right\}} \\ $$$${Similarly},\:\:\:\:{a}_{\mathrm{1}} =\frac{\mathrm{6}\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}}{\mathrm{3}\left\{\left({u}_{\mathrm{2}} \right)^{\mathrm{2}} −\left({u}_{\mathrm{1}} \right)^{\mathrm{2}} \right\}} \\ $$$${I}\:{think}\:{u}_{\mathrm{1}} \:{and}\:{u}_{\mathrm{2}} \:{should}\:{be}\:{taken}\:{as}\:{arbitrary}\:{constants}. \\ $$$${Or}\:{otherwise}\:{if}\:{a}_{\mathrm{1}} \:{and}\:\:{a}_{\mathrm{2}} \:\:{are}\:{taken}\:{as}\:\:{arbitrary}\:{then} \\ $$$${u}_{\mathrm{1}} \:\:{and}\:\:{u}_{\mathrm{2}} \:\:{can}\:{be}\:{determined}. \\ $$$$ \\ $$
