Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214098 by issac last updated on 28/Nov/24

Let F be Field of characteristic 0 L_i (i=1,2) be two algebraic extension of F , and L_1 L_2 be a field in F^� (where F^� is the algebraic closure of F) defined by {l_1 l_2 ∣l_i ∈L_i (i=1,2)} 1. show that if L_1 and L_2 are galois over F then L_1 L_2 is also Galois over F 2. show that if G(L_1 /F^ ) and G(L_2 /F^ ) are Solvable , then Gal(L_1 L_2 /F^ ) is also Solvable

$$\mathrm{Let}\:{F}\:\mathrm{be}\:\:\mathrm{Field}\:\mathrm{of}\:\mathrm{characteristic}\:\mathrm{0} \\ $$$${L}_{{i}} \:\left({i}=\mathrm{1},\mathrm{2}\right)\:\mathrm{be}\:\mathrm{two}\:\mathrm{algebraic}\:\mathrm{extension} \\ $$$$\mathrm{of}\:{F}\:,\:\mathrm{and}\:{L}_{\mathrm{1}} {L}_{\mathrm{2}} \:\mathrm{be}\:\mathrm{a}\:\mathrm{field}\:\mathrm{in}\:\bar {{F}}\: \\ $$$$\left(\mathrm{where}\:\bar {{F}}\:\:\mathrm{is}\:\mathrm{the}\:\mathrm{algebraic}\:\mathrm{closure}\:\:\mathrm{of}\:{F}\right) \\ $$$$\mathrm{defined}\:\mathrm{by}\:\left\{{l}_{\mathrm{1}} {l}_{\mathrm{2}} \mid{l}_{{i}} \in{L}_{{i}} \:\left({i}=\mathrm{1},\mathrm{2}\right)\right\} \\ $$$$\mathrm{1}.\:\mathrm{show}\:\mathrm{that}\:\mathrm{if}\:{L}_{\mathrm{1}} \:\mathrm{and}\:{L}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{galois}\:\mathrm{over}\:{F} \\ $$$$\mathrm{then}\:{L}_{\mathrm{1}} {L}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{also}\:\mathrm{Galois}\:\mathrm{over}\:{F} \\ $$$$\mathrm{2}.\:\mathrm{show}\:\mathrm{that}\:\mathrm{if}\:{G}\left({L}_{\mathrm{1}} /{F}^{\:} \right)\:\mathrm{and}\:{G}\left({L}_{\mathrm{2}} /{F}^{\:} \right) \\ $$$$\mathrm{are}\:\mathrm{Solvable}\:,\:\mathrm{then}\:\mathrm{Gal}\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} /{F}^{\:} \right)\:\mathrm{is}\:\mathrm{also} \\ $$$$\mathrm{Solvable} \\ $$

Answered by MrGaster last updated on 24/Dec/24

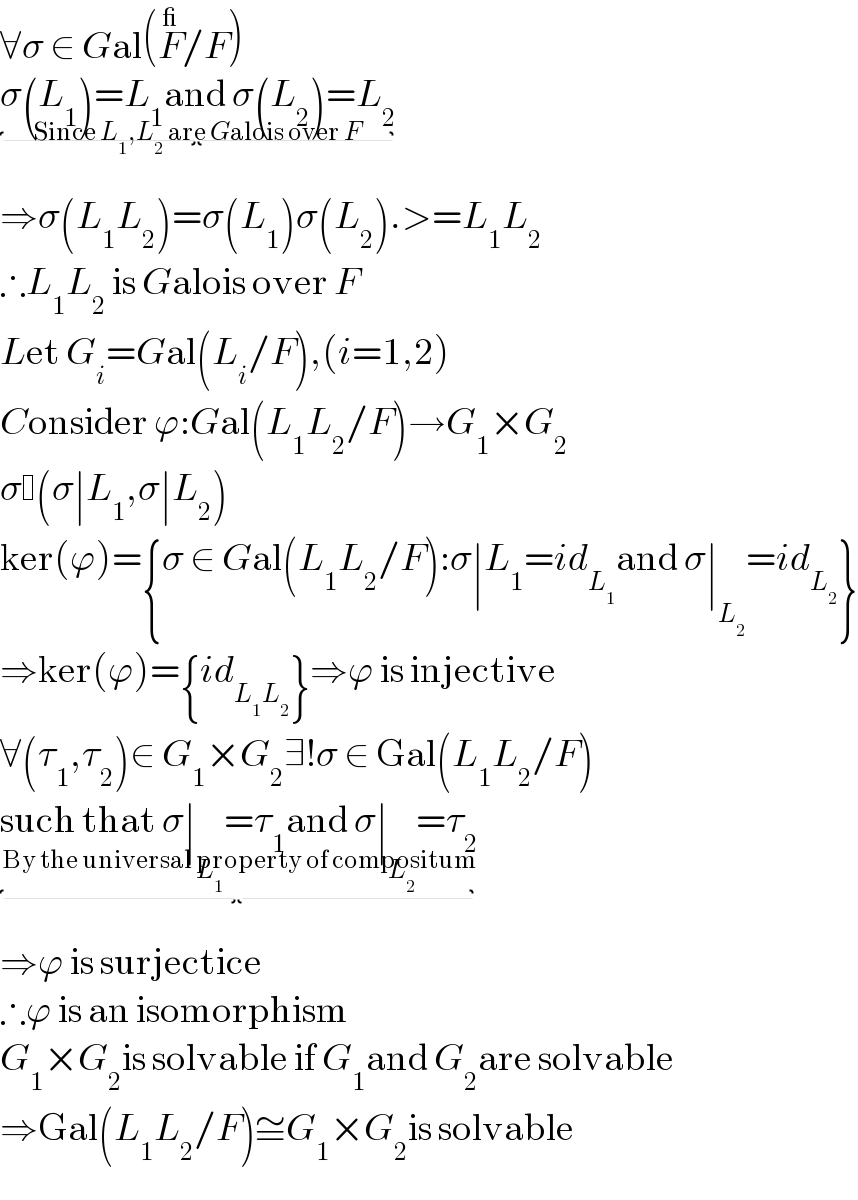
∀σ ∈ Gal(F^_ /F) σ(L_1 )=L_1 and σ(L_2 )=L_2 _(Since L_1 ,L_2 are Galois over F) ⇒σ(L_1 L_2 )=σ(L_1 )σ(L_2 ).>=L_1 L_2 ∴L_1 L_2 is Galois over F Let G_i =Gal(L_i /F),(i=1,2) Consider ϕ:Gal(L_1 L_2 /F)→G_1 ×G_2 σ (σ∣L_1 ,σ∣L_2 ) ker(ϕ)={σ ∈ Gal(L_1 L_2 /F):σ∣L_1 =id_L_1 and σ∣_L_2 =id_L_2 } ⇒ker(ϕ)={id_(L_1 L_2 ) }⇒ϕ is injective ∀(τ_1 ,τ_2 )∈ G_1 ×G_2 ∃!σ ∈ Gal(L_1 L_2 /F) such that σ∣_L_1 =τ_1 and σ∣_L_2 =τ_2 _(By the universal property of compositum) ⇒ϕ is surjectice ∴ϕ is an isomorphism G_1 ×G_2 is solvable if G_1 and G_2 are solvable ⇒Gal(L_1 L_2 /F)≅G_1 ×G_2 is solvable

$$\forall\sigma\:\in\:{G}\mathrm{al}\left(\overset{\_} {{F}}/{F}\right) \\ $$$$\underset{\mathrm{Since}\:{L}_{\mathrm{1}} ,{L}_{\mathrm{2}} \:\mathrm{are}\:{G}\mathrm{alois}\:\mathrm{over}\:{F}} {\underbrace{\sigma\left({L}_{\mathrm{1}} \right)={L}_{\mathrm{1}} \mathrm{and}\:\sigma\left({L}_{\mathrm{2}} \right)={L}_{\mathrm{2}} }} \\ $$$$\Rightarrow\sigma\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} \right)=\sigma\left({L}_{\mathrm{1}} \right)\sigma\left({L}_{\mathrm{2}} \right).>={L}_{\mathrm{1}} {L}_{\mathrm{2}} \\ $$$$\therefore{L}_{\mathrm{1}} {L}_{\mathrm{2}} \:\mathrm{is}\:{G}\mathrm{alois}\:\mathrm{over}\:{F} \\ $$$${L}\mathrm{et}\:{G}_{{i}} ={G}\mathrm{al}\left({L}_{{i}} /{F}\right),\left({i}=\mathrm{1},\mathrm{2}\right) \\ $$$${C}\mathrm{onsider}\:\varphi:{G}\mathrm{al}\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} /{F}\right)\rightarrow{G}_{\mathrm{1}} ×{G}_{\mathrm{2}} \\ $$$$\sigma \left(\sigma\mid{L}_{\mathrm{1}} ,\sigma\mid{L}_{\mathrm{2}} \right) \\ $$$$\mathrm{ker}\left(\varphi\right)=\left\{\sigma\:\in\:{G}\mathrm{al}\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} /{F}\right):\sigma\mid{L}_{\mathrm{1}} ={id}_{{L}_{\mathrm{1}} } \mathrm{and}\:\sigma\mid_{{L}_{\mathrm{2}} } ={id}_{{L}_{\mathrm{2}} } \right\} \\ $$$$\Rightarrow\mathrm{ker}\left(\varphi\right)=\left\{{id}_{{L}_{\mathrm{1}} {L}_{\mathrm{2}} } \right\}\Rightarrow\varphi\:\mathrm{is}\:\mathrm{injective} \\ $$$$\forall\left(\tau_{\mathrm{1}} ,\tau_{\mathrm{2}} \right)\in\:{G}_{\mathrm{1}} ×{G}_{\mathrm{2}} \exists!\sigma\:\in\:\mathrm{Gal}\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} /{F}\right) \\ $$$$\underset{\mathrm{By}\:\mathrm{the}\:\mathrm{universal}\:\mathrm{property}\:\mathrm{of}\:\mathrm{compositum}} {\underbrace{\mathrm{such}\:\mathrm{that}\:\sigma\mid_{{L}_{\mathrm{1}} } =\tau_{\mathrm{1}} \mathrm{and}\:\sigma\mid_{{L}_{\mathrm{2}} } =\tau_{\mathrm{2}} }} \\ $$$$\Rightarrow\varphi\:\mathrm{is}\:\mathrm{surjectice} \\ $$$$\therefore\varphi\:\mathrm{is}\:\mathrm{an}\:\mathrm{isomorphism} \\ $$$${G}_{\mathrm{1}} ×{G}_{\mathrm{2}} \mathrm{is}\:\mathrm{solvable}\:\mathrm{if}\:{G}_{\mathrm{1}} \mathrm{and}\:{G}_{\mathrm{2}} \mathrm{are}\:\mathrm{solvable} \\ $$$$\Rightarrow\mathrm{Gal}\left({L}_{\mathrm{1}} {L}_{\mathrm{2}} /{F}\right)\cong{G}_{\mathrm{1}} ×{G}_{\mathrm{2}} \mathrm{is}\:\mathrm{solvable} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com