Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16071 by Tinkutara last updated on 21/Jun/17

Let A′, B′ and C′ be points on the sides BC, CA and AB of the triangle ABC. Prove that the circumcircles of the triangles AB′C′, BA′C′ and CA′B′ have a common point. Prove that the property holds even if the points A′, B′ and C′ are collinear.

$$\mathrm{Let}\:{A}',\:{B}'\:\mathrm{and}\:{C}'\:\mathrm{be}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the}\:\mathrm{sides} \\ $$$${BC},\:{CA}\:\mathrm{and}\:{AB}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:{ABC}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{circumcircles}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangles}\:{AB}'{C}',\:{BA}'{C}'\:\mathrm{and}\:{CA}'{B}' \\ $$$$\mathrm{have}\:\mathrm{a}\:\mathrm{common}\:\mathrm{point}.\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{property}\:\mathrm{holds}\:\mathrm{even}\:\mathrm{if}\:\mathrm{the}\:\mathrm{points}\:{A}', \\ $$$${B}'\:\mathrm{and}\:{C}'\:\mathrm{are}\:\mathrm{collinear}. \\ $$

Answered by mrW1 last updated on 05/Jul/17

Commented by mrW1 last updated on 05/Jul/17

Commented by mrW1 last updated on 05/Jul/17

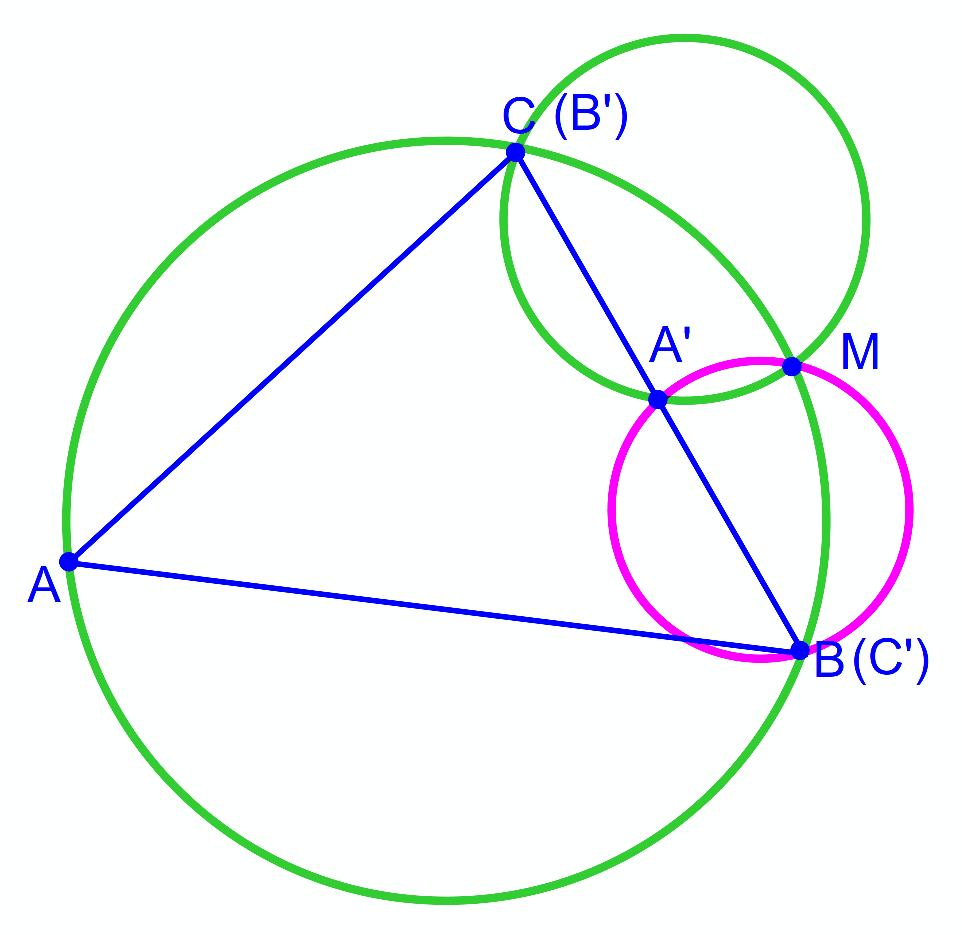
B′A′C′ are colinear. O_(ΔAB′C′) and O_(ΔCA′B′) intersect at M. Through B,C′,A′ and M one can always construct a circle. ⇒all 3 circles have always a common point M, even more than one.

$$\mathrm{B}'\mathrm{A}'\mathrm{C}'\:\mathrm{are}\:\mathrm{colinear}. \\ $$$$\mathrm{O}_{\Delta\mathrm{AB}'\mathrm{C}'} \:\mathrm{and}\:\mathrm{O}_{\Delta\mathrm{CA}'\mathrm{B}'} \:\mathrm{intersect}\:\mathrm{at}\:\mathrm{M}. \\ $$$$\mathrm{Through}\:\mathrm{B},\mathrm{C}',\mathrm{A}'\:\mathrm{and}\:\mathrm{M}\:\mathrm{one}\:\mathrm{can}\:\mathrm{always} \\ $$$$\mathrm{construct}\:\mathrm{a}\:\mathrm{circle}. \\ $$$$\Rightarrow\mathrm{all}\:\mathrm{3}\:\mathrm{circles}\:\mathrm{have}\:\mathrm{always}\:\mathrm{a}\:\mathrm{common} \\ $$$$\mathrm{point}\:\mathrm{M},\:\mathrm{even}\:\mathrm{more}\:\mathrm{than}\:\mathrm{one}. \\ $$

Commented by mrW1 last updated on 05/Jul/17

O_(ΔAB′C′) and O_(ΔCA′B′) intersect at M. ∠B′MC′=180°−∠A ∠B′MA′=180°−∠C ⇒∠B′MC′=360°−∠B′MA′−∠B′MC′ =360°−(180°−∠C+180°−∠A) =∠A+∠C ∠B′MC′+∠B=∠A+∠C+∠B=180° ⇒A′BC′M is cyclic. ⇒M lies on circle O_(ΔBA′C′) ⇒ all circles have a common point M.

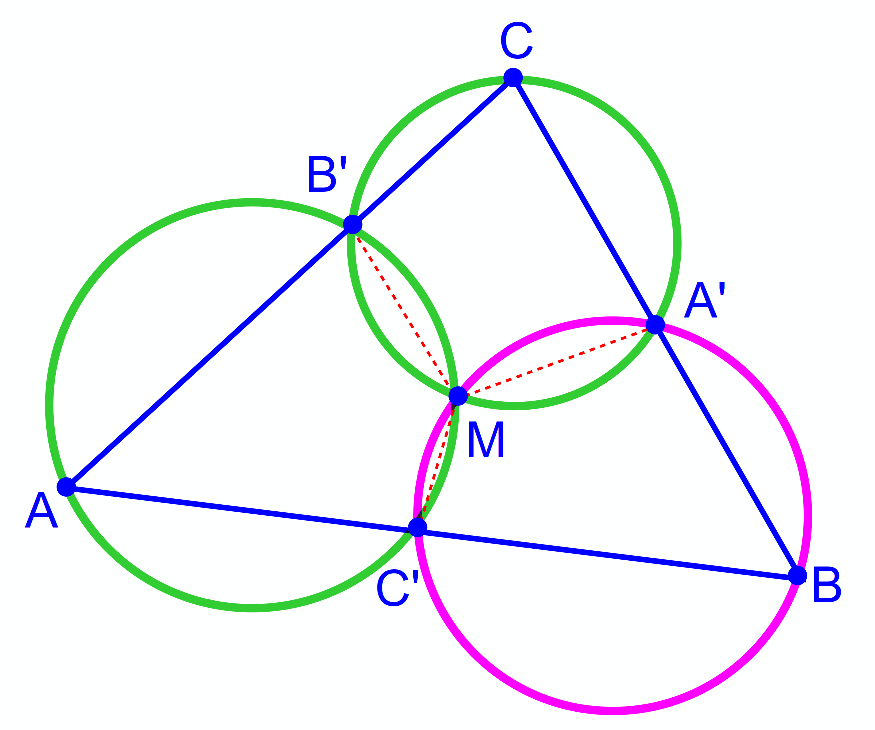
$$\mathrm{O}_{\Delta\mathrm{AB}'\mathrm{C}'} \:\mathrm{and}\:\mathrm{O}_{\Delta\mathrm{CA}'\mathrm{B}'} \:\mathrm{intersect}\:\mathrm{at}\:\mathrm{M}. \\ $$$$\angle\mathrm{B}'\mathrm{MC}'=\mathrm{180}°−\angle\mathrm{A} \\ $$$$\angle\mathrm{B}'\mathrm{MA}'=\mathrm{180}°−\angle\mathrm{C} \\ $$$$\Rightarrow\angle\mathrm{B}'\mathrm{MC}'=\mathrm{360}°−\angle\mathrm{B}'\mathrm{MA}'−\angle\mathrm{B}'\mathrm{MC}' \\ $$$$=\mathrm{360}°−\left(\mathrm{180}°−\angle\mathrm{C}+\mathrm{180}°−\angle\mathrm{A}\right) \\ $$$$=\angle\mathrm{A}+\angle\mathrm{C} \\ $$$$ \\ $$$$\angle\mathrm{B}'\mathrm{MC}'+\angle\mathrm{B}=\angle\mathrm{A}+\angle\mathrm{C}+\angle\mathrm{B}=\mathrm{180}° \\ $$$$\Rightarrow\mathrm{A}'\mathrm{BC}'\mathrm{M}\:\mathrm{is}\:\mathrm{cyclic}. \\ $$$$\Rightarrow\mathrm{M}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{circle}\:\mathrm{O}_{\Delta\mathrm{BA}'\mathrm{C}'} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{all}\:\mathrm{circles}\:\mathrm{have}\:\mathrm{a}\:\mathrm{common}\:\mathrm{point}\:\mathrm{M}. \\ $$

Commented by Tinkutara last updated on 05/Jul/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com