Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 34063 by rahul 19 last updated on 30/Apr/18

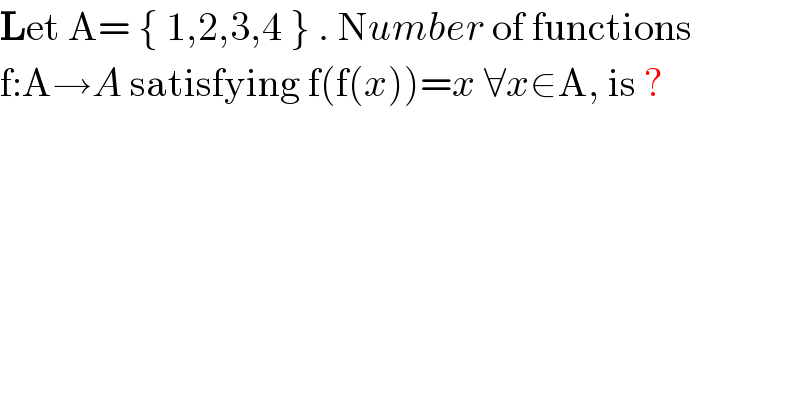
Let A= { 1,2,3,4 } . Number of functions f:A→A satisfying f(f(x))=x ∀x∈A, is ?

$$\boldsymbol{\mathrm{L}}\mathrm{et}\:\mathrm{A}=\:\left\{\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:\right\}\:.\:\mathrm{N}{umber}\:\mathrm{of}\:\mathrm{functions} \\ $$$$\mathrm{f}:\mathrm{A}\rightarrow{A}\:\mathrm{satisfying}\:\mathrm{f}\left(\mathrm{f}\left({x}\right)\right)={x}\:\forall{x}\in\mathrm{A},\:\mathrm{is}\:? \\ $$

Commented by rahul 19 last updated on 30/Apr/18

Ans. is 13....

$${Ans}.\:{is}\:\mathrm{13}.... \\ $$

Commented by rahul 19 last updated on 30/Apr/18

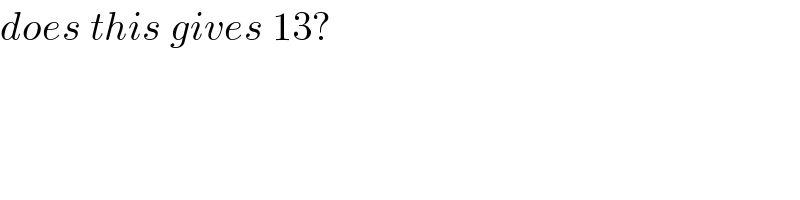
does this gives 13?

$${does}\:{this}\:{gives}\:\mathrm{13}? \\ $$

Commented by Rasheed.Sindhi last updated on 30/Apr/18

For example: {(1,2),(2,1),(3,4),(4,3)} f(1)=2, f( f(1) )=f(2)=1 f( f(2) )=f(1)=2 a,b,c,d∈A , a,b,c,d are different {(a,a),(b,b),(c,c),(d,d)} {(a,a),(b,b),(c,d),(d,c)} {(a,b),(b,a),(c,d),(d,c)} Continue

$$\mathrm{For}\:\mathrm{example}: \\ $$$$\:\:\:\:\:\:\left\{\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{4},\mathrm{3}\right)\right\} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2},\:\mathrm{f}\left(\:\mathrm{f}\left(\mathrm{1}\right)\:\right)=\mathrm{f}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$$\mathrm{f}\left(\:\mathrm{f}\left(\mathrm{2}\right)\:\right)=\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:{a},{b},{c},{d}\in\mathrm{A}\:,\:{a},{b},{c},{d}\:\mathrm{are}\:\mathrm{different} \\ $$$$\:\:\:\:\:\:\:\left\{\left({a},{a}\right),\left({b},{b}\right),\left({c},{c}\right),\left({d},{d}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\left\{\left({a},{a}\right),\left({b},{b}\right),\left({c},{d}\right),\left({d},{c}\right)\right\} \\ $$$$\:\:\:\:\:\:\left\{\left({a},{b}\right),\left({b},{a}\right),\left({c},{d}\right),\left({d},{c}\right)\right\} \\ $$$$ \\ $$$$\mathrm{Continue} \\ $$

Answered by Rasheed.Sindhi last updated on 30/Apr/18

Domain(f)=A, the function have 4 orderd pairs, the pair of f is either of (a,a) type or if it is (a,b) with a≠b then the f also contains (b,a) because of the condition f(f(x))=x ∀x∈A. The ordered pair containing 1 as abscissa may be (1,1),(1,2),(1,3),(1,4) (1,1):(2,2),(2,3),(2,4) [(2,1) is impossible −−−−−− (1,1),(2,2),(3,3),(4,4) (1,1),(2,2),(3,4),(4,3) (1,1),(2,3),(3,2),(4,4) (1,1),(2,4),(3,3),(4,2) −−−−− (1,2),(2,1),(3,4),(4,3) (1,2),(2,1),(3,3),(4,4) (1,3),(2,4),(3,1),(4,2) (1,3),(2,2),(3,1),(4,4) (1,4)(2,3)(3,2),(4,1) (1,4)(2,2)(3,3),(4,1)

$$\mathrm{Domain}\left(\mathrm{f}\right)=\mathrm{A},\:\mathrm{the}\:\mathrm{function}\:\mathrm{have}\:\mathrm{4}\:\mathrm{orderd} \\ $$$$\mathrm{pairs},\:\mathrm{the}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{f}\:\mathrm{is}\:\mathrm{either}\:\mathrm{of}\:\left({a},{a}\right)\:\mathrm{type} \\ $$$$\mathrm{or}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\left({a},{b}\right)\:\mathrm{with}\:{a}\neq\mathrm{b}\:\mathrm{then}\:\mathrm{the}\:\mathrm{f}\:\mathrm{also} \\ $$$$\mathrm{contains}\:\left({b},{a}\right)\:\mathrm{because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{condition} \\ $$$$\mathrm{f}\left(\mathrm{f}\left({x}\right)\right)={x}\:\forall{x}\in\mathrm{A}. \\ $$$$\:\:\:\:\:\:\:\mathrm{The}\:\mathrm{ordered}\:\mathrm{pair}\:\mathrm{containing}\:\mathrm{1}\:\mathrm{as}\:\mathrm{abscissa} \\ $$$$\mathrm{may}\:\mathrm{be}\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{1},\mathrm{3}\right),\left(\mathrm{1},\mathrm{4}\right) \\ $$$$\:\left(\mathrm{1},\mathrm{1}\right):\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{2},\mathrm{4}\right)\:\left[\left(\mathrm{2},\mathrm{1}\right)\:\mathrm{is}\:\mathrm{impossible}\right. \\ $$$$−−−−−− \\ $$$$\:\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{3},\mathrm{3}\right),\left(\mathrm{4},\mathrm{4}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{4},\mathrm{3}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{3},\mathrm{2}\right),\left(\mathrm{4},\mathrm{4}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{4}\right),\left(\mathrm{3},\mathrm{3}\right),\left(\mathrm{4},\mathrm{2}\right) \\ $$$$−−−−− \\ $$$$\:\:\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{4},\mathrm{3}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{3},\mathrm{3}\right),\left(\mathrm{4},\mathrm{4}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{3}\right),\left(\mathrm{2},\mathrm{4}\right),\left(\mathrm{3},\mathrm{1}\right),\left(\mathrm{4},\mathrm{2}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{3}\right),\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{3},\mathrm{1}\right),\left(\mathrm{4},\mathrm{4}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{4}\right)\left(\mathrm{2},\mathrm{3}\right)\left(\mathrm{3},\mathrm{2}\right),\left(\mathrm{4},\mathrm{1}\right) \\ $$$$\:\:\left(\mathrm{1},\mathrm{4}\right)\left(\mathrm{2},\mathrm{2}\right)\left(\mathrm{3},\mathrm{3}\right),\left(\mathrm{4},\mathrm{1}\right) \\ $$$$\: \\ $$

Commented by Rasheed.Sindhi last updated on 30/Apr/18

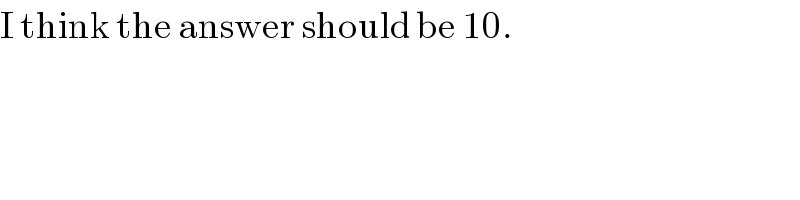
I think the answer should be 10.

$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{be}\:\mathrm{10}. \\ $$

Commented by rahul 19 last updated on 30/Apr/18

Thank You Sir !

$$\mathscr{T}{hank}\:\mathscr{Y}{ou}\:\mathscr{S}{ir}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com