
Question Number 63942 by gunawan last updated on 11/Jul/19
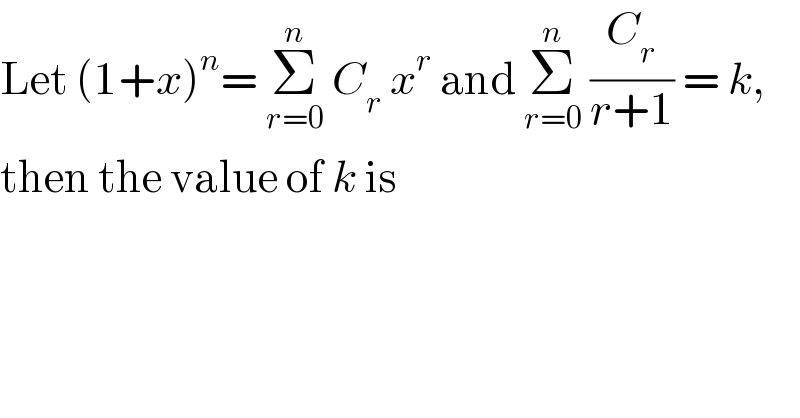
$$\mathrm{Let}\:\left(\mathrm{1}+{x}\right)^{{n}} =\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}_{{r}} \:{x}^{{r}} \:\mathrm{and}\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{{C}_{{r}} }{{r}+\mathrm{1}}\:=\:{k}, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{k}\:\mathrm{is} \\ $$
Commented by mathmax by abdo last updated on 11/Jul/19
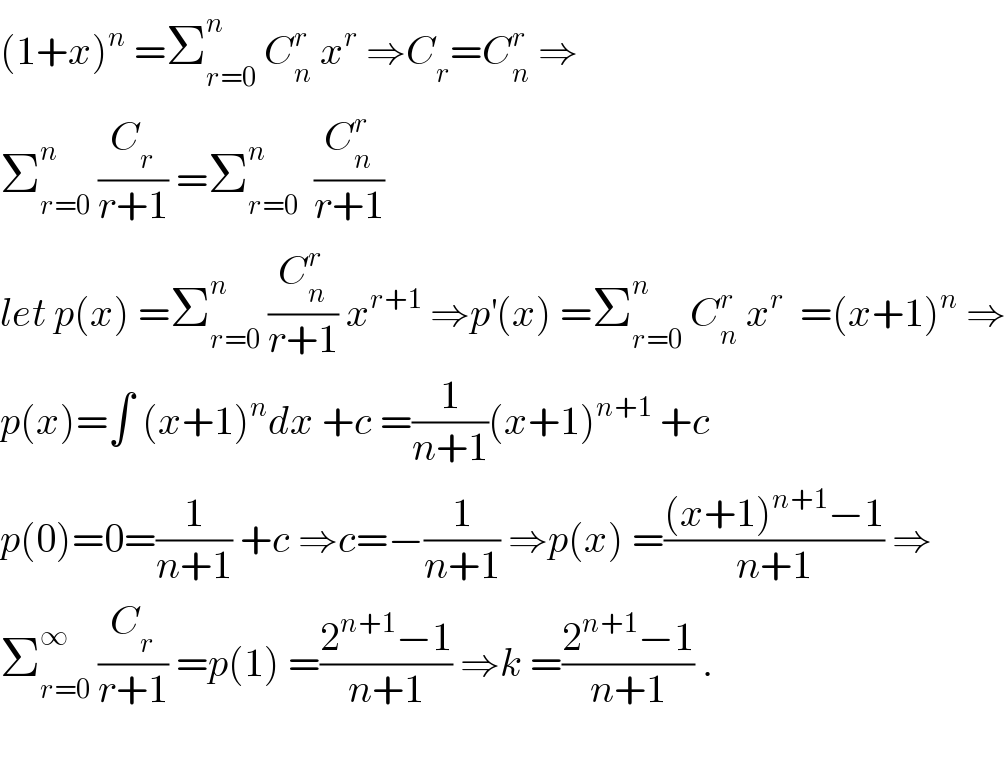
$$\left(\mathrm{1}+{x}\right)^{{n}} \:=\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:\Rightarrow{C}_{{r}} ={C}_{{n}} ^{{r}} \:\Rightarrow \\ $$$$\sum_{{r}=\mathrm{0}} ^{{n}} \:\frac{{C}_{{r}} }{{r}+\mathrm{1}}\:=\sum_{{r}=\mathrm{0}} ^{{n}} \:\:\frac{{C}_{{n}} ^{{r}} }{{r}+\mathrm{1}} \\ $$$${let}\:{p}\left({x}\right)\:=\sum_{{r}=\mathrm{0}} ^{{n}} \:\frac{{C}_{{n}} ^{{r}} }{{r}+\mathrm{1}}\:{x}^{{r}+\mathrm{1}} \:\Rightarrow{p}^{'} \left({x}\right)\:=\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:\:=\left({x}+\mathrm{1}\right)^{{n}} \:\Rightarrow \\ $$$${p}\left({x}\right)=\int\:\left({x}+\mathrm{1}\right)^{{n}} {dx}\:+{c}\:=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left({x}+\mathrm{1}\right)^{{n}+\mathrm{1}} \:+{c} \\ $$$${p}\left(\mathrm{0}\right)=\mathrm{0}=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:+{c}\:\Rightarrow{c}=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow{p}\left({x}\right)\:=\frac{\left({x}+\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{r}=\mathrm{0}} ^{\infty} \:\frac{{C}_{{r}} }{{r}+\mathrm{1}}\:={p}\left(\mathrm{1}\right)\:=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow{k}\:=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:. \\ $$$$ \\ $$
Answered by mr W last updated on 11/Jul/19
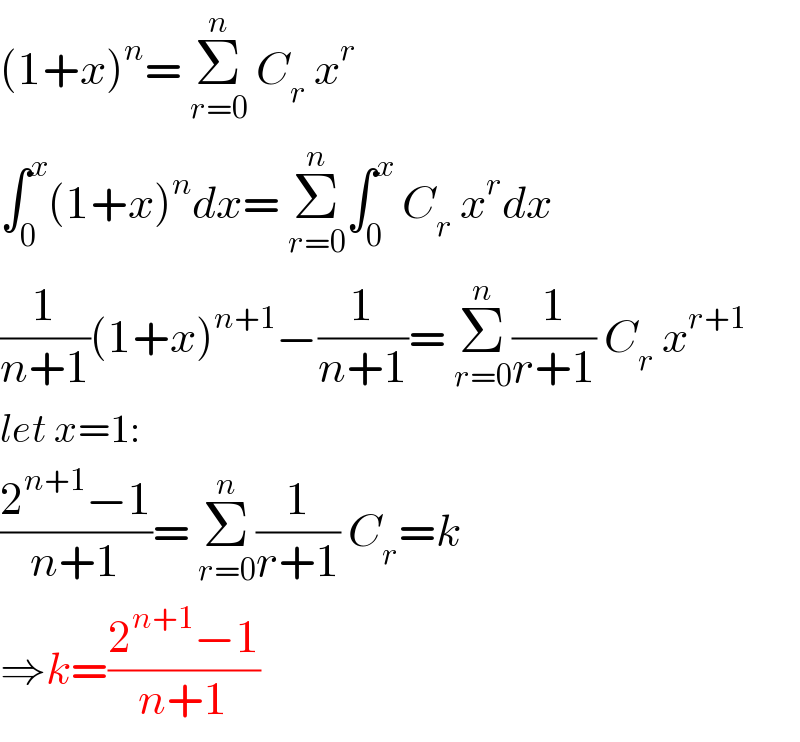
$$\left(\mathrm{1}+{x}\right)^{{n}} =\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}_{{r}} \:{x}^{{r}} \\ $$$$\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}+{x}\right)^{{n}} {dx}=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{{x}} \:{C}_{{r}} \:{x}^{{r}} {dx} \\ $$$$\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}+\mathrm{1}}\:{C}_{{r}} \:{x}^{{r}+\mathrm{1}} \\ $$$${let}\:{x}=\mathrm{1}: \\ $$$$\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}+\mathrm{1}}\:{C}_{{r}} ={k}\: \\ $$$$\Rightarrow{k}=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}} \\ $$
