Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 93982 by Rasheed.Sindhi last updated on 16/May/20

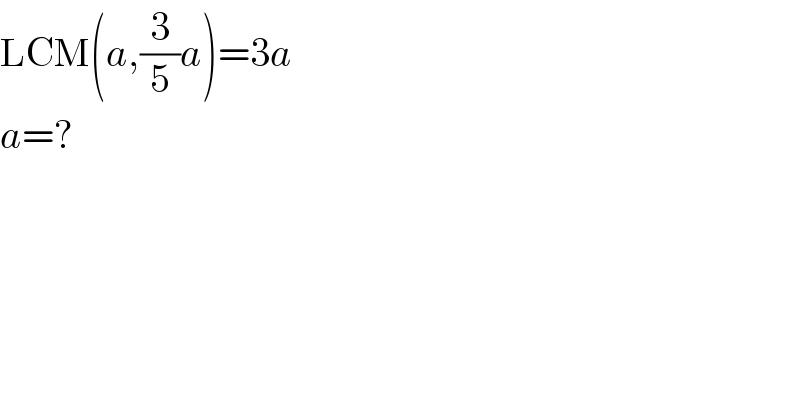
LCM(a,(3/5)a)=3a a=?

$$\mathrm{LCM}\left({a},\frac{\mathrm{3}}{\mathrm{5}}{a}\right)=\mathrm{3}{a}\: \\ $$$${a}=? \\ $$

Commented by mr W last updated on 16/May/20

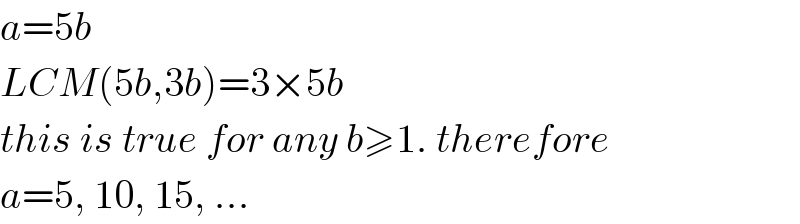
a=5b LCM(5b,3b)=3×5b this is true for any b≥1. therefore a=5, 10, 15, ...

$${a}=\mathrm{5}{b} \\ $$$${LCM}\left(\mathrm{5}{b},\mathrm{3}{b}\right)=\mathrm{3}×\mathrm{5}{b} \\ $$$${this}\:{is}\:{true}\:{for}\:{any}\:{b}\geqslant\mathrm{1}.\:{therefore} \\ $$$${a}=\mathrm{5},\:\mathrm{10},\:\mathrm{15},\:... \\ $$

Commented by PRITHWISH SEN 2 last updated on 16/May/20

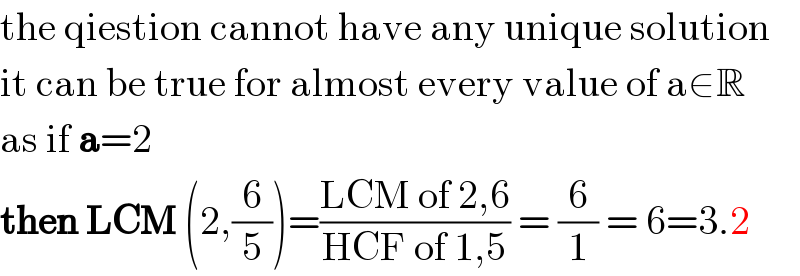
the qiestion cannot have any unique solution it can be true for almost every value of a∈R as if a=2 then LCM (2,(6/5))=((LCM of 2,6)/(HCF of 1,5)) = (6/1) = 6=3.2

$$\mathrm{the}\:\mathrm{qiestion}\:\mathrm{cannot}\:\mathrm{have}\:\mathrm{any}\:\mathrm{unique}\:\mathrm{solution} \\ $$$$\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{true}\:\mathrm{for}\:\mathrm{almost}\:\mathrm{every}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}\in\mathbb{R} \\ $$$$\mathrm{as}\:\mathrm{if}\:\boldsymbol{\mathrm{a}}=\mathrm{2} \\ $$$$\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{LCM}}\:\left(\mathrm{2},\frac{\mathrm{6}}{\mathrm{5}}\right)=\frac{\mathrm{LCM}\:\mathrm{of}\:\mathrm{2},\mathrm{6}}{\mathrm{HCF}\:\mathrm{of}\:\mathrm{1},\mathrm{5}}\:=\:\frac{\mathrm{6}}{\mathrm{1}}\:=\:\mathrm{6}=\mathrm{3}.\mathrm{2} \\ $$

Commented by mr W last updated on 16/May/20

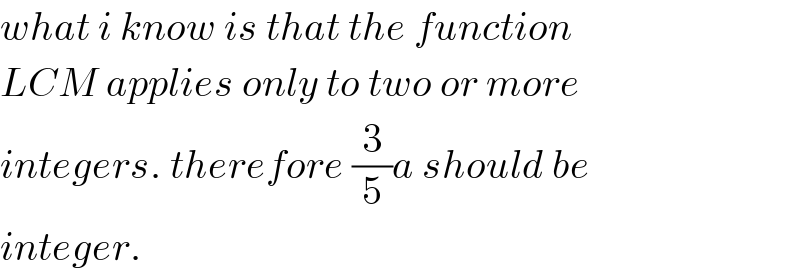
what i know is that the function LCM applies only to two or more integers. therefore (3/5)a should be integer.

$${what}\:{i}\:{know}\:{is}\:{that}\:{the}\:{function} \\ $$$${LCM}\:{applies}\:{only}\:{to}\:{two}\:{or}\:{more} \\ $$$${integers}.\:{therefore}\:\frac{\mathrm{3}}{\mathrm{5}}{a}\:{should}\:{be} \\ $$$${integer}. \\ $$

Commented by PRITHWISH SEN 2 last updated on 16/May/20

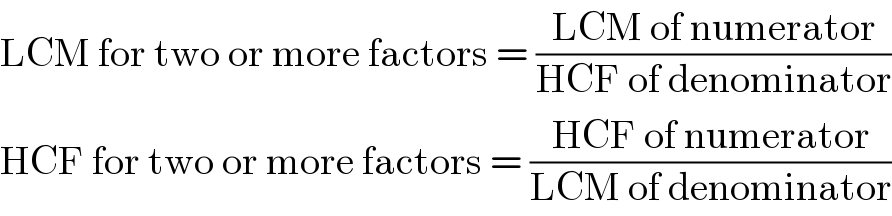
LCM for two or more factors = ((LCM of numerator)/(HCF of denominator)) HCF for two or more factors = ((HCF of numerator)/(LCM of denominator))

$$\mathrm{LCM}\:\mathrm{for}\:\mathrm{two}\:\mathrm{or}\:\mathrm{more}\:\mathrm{factors}\:=\:\frac{\mathrm{LCM}\:\mathrm{of}\:\mathrm{numerator}}{\mathrm{HCF}\:\mathrm{of}\:\mathrm{denominator}} \\ $$$$\mathrm{HCF}\:\mathrm{for}\:\mathrm{two}\:\mathrm{or}\:\mathrm{more}\:\mathrm{factors}\:=\:\frac{\mathrm{HCF}\:\mathrm{of}\:\mathrm{numerator}}{\mathrm{LCM}\:\mathrm{of}\:\mathrm{denominator}} \\ $$

Commented by mr W last updated on 16/May/20

thanks sir!

$${thanks}\:{sir}! \\ $$

Commented by PRITHWISH SEN 2 last updated on 16/May/20

welcome sir.

$$\mathrm{welcome}\:\mathrm{sir}. \\ $$

Commented by Rasheed.Sindhi last updated on 16/May/20

Thank you all sirs!

$${Thank}\:{you}\:{all}\:{sirs}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com