Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 120914 by SOMEDAVONG last updated on 04/Nov/20

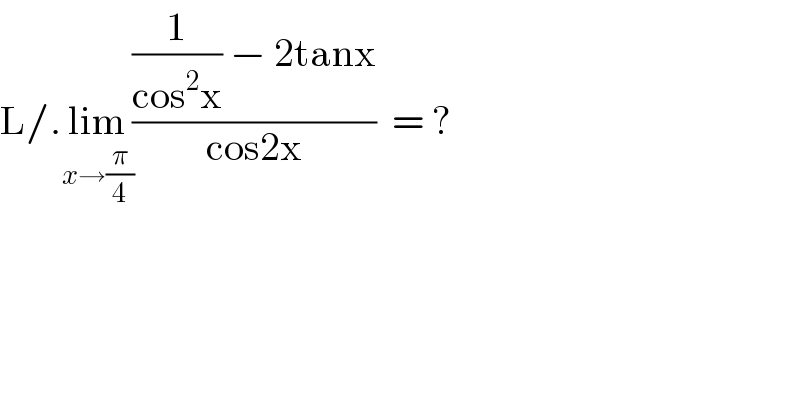
L/.lim_(x→(π/4)) (((1/(cos^2 x)) − 2tanx)/(cos2x)) = ?

$$\mathrm{L}/.\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:−\:\mathrm{2tanx}}{\mathrm{cos2x}}\:\:=\:? \\ $$

Answered by bemath last updated on 04/Nov/20

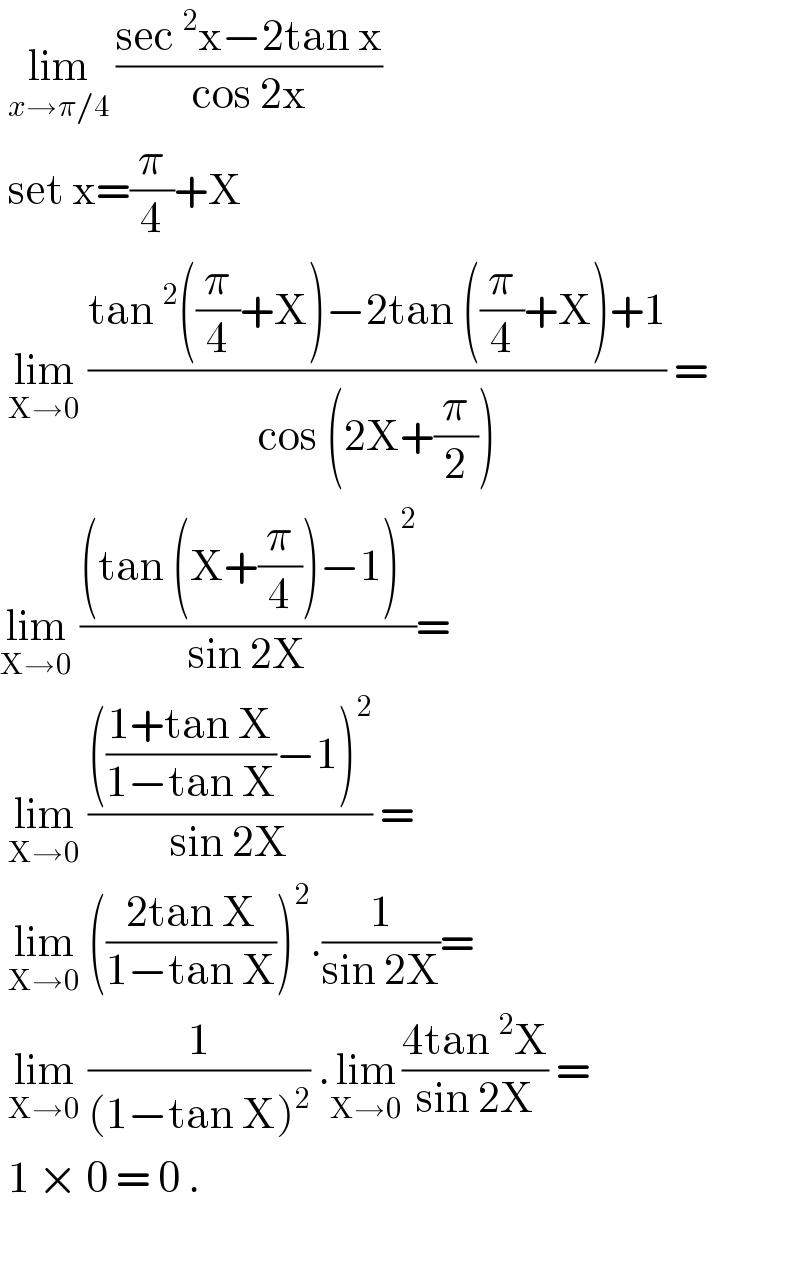
lim_(x→π/4) ((sec^2 x−2tan x)/(cos 2x)) set x=(π/4)+X lim_(X→0) ((tan^2 ((π/4)+X)−2tan ((π/4)+X)+1)/(cos (2X+(π/2)))) = lim_(X→0) (((tan (X+(π/4))−1)^2 )/(sin 2X))= lim_(X→0) (((((1+tan X)/(1−tan X))−1)^2 )/(sin 2X)) = lim_(X→0) (((2tan X)/(1−tan X)))^2 .(1/(sin 2X))= lim_(X→0) (1/((1−tan X)^2 )) .lim_(X→0) ((4tan^2 X)/(sin 2X)) = 1 × 0 = 0 .

$$\:\underset{{x}\rightarrow\pi/\mathrm{4}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{2tan}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{2x}} \\ $$$$\:\mathrm{set}\:\mathrm{x}=\frac{\pi}{\mathrm{4}}+\mathrm{X} \\ $$$$\:\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}+\mathrm{X}\right)−\mathrm{2tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{X}\right)+\mathrm{1}}{\mathrm{cos}\:\left(\mathrm{2X}+\frac{\pi}{\mathrm{2}}\right)}\:= \\ $$$$\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{tan}\:\left(\mathrm{X}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{sin}\:\mathrm{2X}}= \\ $$$$\:\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{X}}{\mathrm{1}−\mathrm{tan}\:\mathrm{X}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{sin}\:\mathrm{2X}}\:= \\ $$$$\:\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2tan}\:\mathrm{X}}{\mathrm{1}−\mathrm{tan}\:\mathrm{X}}\right)^{\mathrm{2}} .\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{2X}}= \\ $$$$\:\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{tan}\:\mathrm{X}\right)^{\mathrm{2}} }\:.\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4tan}\:^{\mathrm{2}} \mathrm{X}}{\mathrm{sin}\:\mathrm{2X}}\:= \\ $$$$\:\mathrm{1}\:×\:\mathrm{0}\:=\:\mathrm{0}\:.\: \\ $$$$ \\ $$

Answered by Jamshidbek2311 last updated on 04/Nov/20

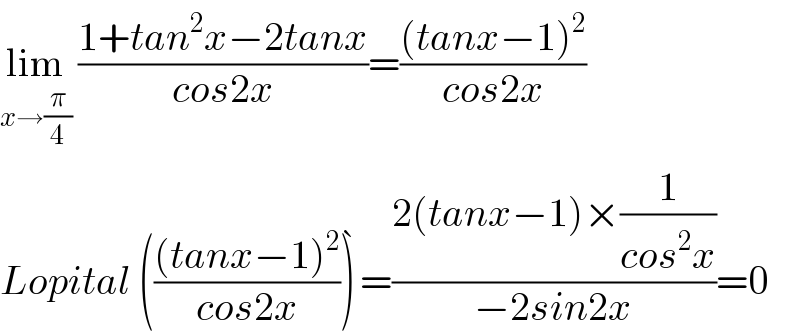
lim_(x→(π/4)) ((1+tan^2 x−2tanx)/(cos2x))=(((tanx−1)^2 )/(cos2x)) Lopital ((((tanx−1)^2 )/(cos2x)))^� =((2(tanx−1)×(1/(cos^2 x)))/(−2sin2x))=0

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}−\mathrm{2}{tanx}}{{cos}\mathrm{2}{x}}=\frac{\left({tanx}−\mathrm{1}\right)^{\mathrm{2}} }{{cos}\mathrm{2}{x}} \\ $$$${Lopital}\:\left(\frac{\left({tanx}−\mathrm{1}\right)^{\mathrm{2}} }{{cos}\mathrm{2}{x}}\grave {\right)}=\frac{\mathrm{2}\left({tanx}−\mathrm{1}\right)×\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}}{−\mathrm{2}{sin}\mathrm{2}{x}}=\mathrm{0} \\ $$

Answered by MJS_new last updated on 04/Nov/20

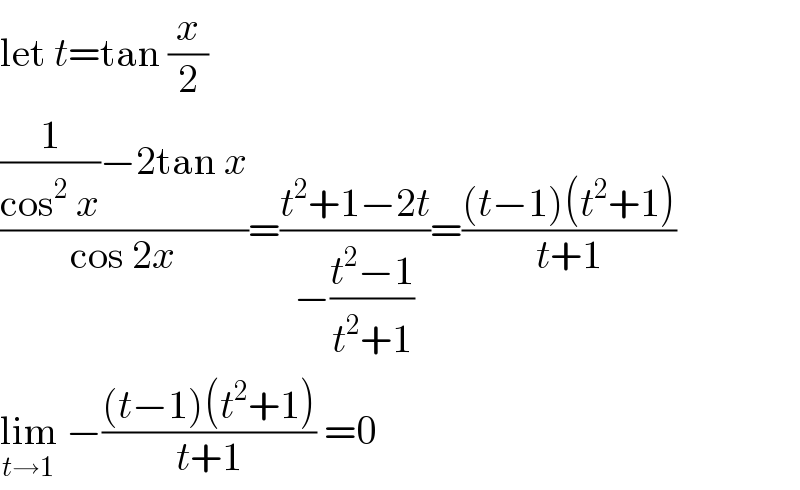
let t=tan (x/2) (((1/(cos^2 x))−2tan x)/(cos 2x))=((t^2 +1−2t)/(−((t^2 −1)/(t^2 +1))))=(((t−1)(t^2 +1))/(t+1)) lim_(t→1) −(((t−1)(t^2 +1))/(t+1)) =0

$$\mathrm{let}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}−\mathrm{2tan}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}=\frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{t}}{−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}}=\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}+\mathrm{1}} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:−\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}+\mathrm{1}}\:=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com