Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 208280 by Shrodinger last updated on 10/Jun/24

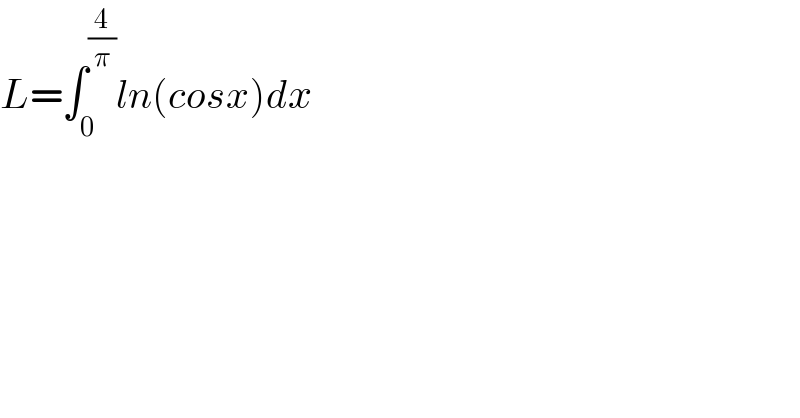
L=∫_0 ^(4/π) ln(cosx)dx

$${L}=\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{\pi}} {ln}\left({cosx}\right){dx} \\ $$

Answered by Berbere last updated on 10/Jun/24

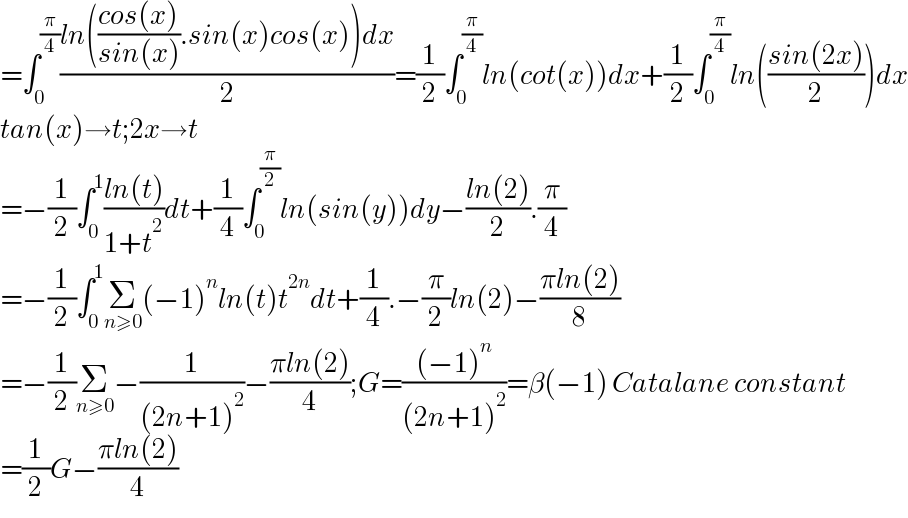
=∫_0 ^(π/4) ((ln(((cos(x))/(sin(x))).sin(x)cos(x))dx)/2)=(1/2)∫_0 ^(π/4) ln(cot(x))dx+(1/2)∫_0 ^(π/4) ln(((sin(2x))/2))dx tan(x)→t;2x→t =−(1/2)∫_0 ^1 ((ln(t))/(1+t^2 ))dt+(1/4)∫_0 ^(π/2) ln(sin(y))dy−((ln(2))/2).(π/4) =−(1/2)∫_0 ^1 Σ_(n≥0) (−1)^n ln(t)t^(2n) dt+(1/4).−(π/2)ln(2)−((πln(2))/8) =−(1/2)Σ_(n≥0) −(1/((2n+1)^2 ))−((πln(2))/4);G=(((−1)^n )/((2n+1)^2 ))=β(−1) Catalane constant =(1/2)G−((πln(2))/4)

$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{ln}\left(\frac{{cos}\left({x}\right)}{{sin}\left({x}\right)}.{sin}\left({x}\right){cos}\left({x}\right)\right){dx}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cot}\left({x}\right)\right){dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$${tan}\left({x}\right)\rightarrow{t};\mathrm{2}{x}\rightarrow{t} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({y}\right)\right){dy}−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}.\frac{\pi}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} {ln}\left({t}\right){t}^{\mathrm{2}{n}} {dt}+\frac{\mathrm{1}}{\mathrm{4}}.−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}};{G}=\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\beta\left(−\mathrm{1}\right)\:{Catalane}\:{constant} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{G}−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$

Commented by Shrodinger last updated on 11/Jun/24

thanks sir..

$${thanks}\:{sir}.. \\ $$

Commented by Shrodinger last updated on 11/Jun/24

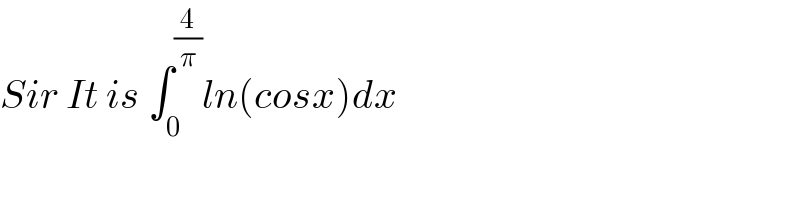
Sir It is ∫_0 ^(4/π) ln(cosx)dx

$${Sir}\:{It}\:{is}\:\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{\pi}} {ln}\left({cosx}\right){dx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com