
Question Number 194257 by tri26112004 last updated on 01/Jul/23
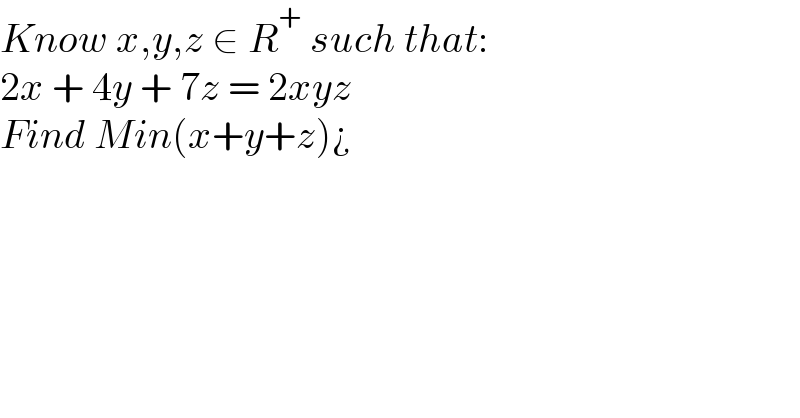
$${Know}\:{x},{y},{z}\:\in\:{R}^{+} \:{such}\:{that}: \\ $$$$\mathrm{2}{x}\:+\:\mathrm{4}{y}\:+\:\mathrm{7}{z}\:=\:\mathrm{2}{xyz} \\ $$$${Find}\:{Min}\left({x}+{y}+{z}\right)¿ \\ $$
Commented by Frix last updated on 01/Jul/23
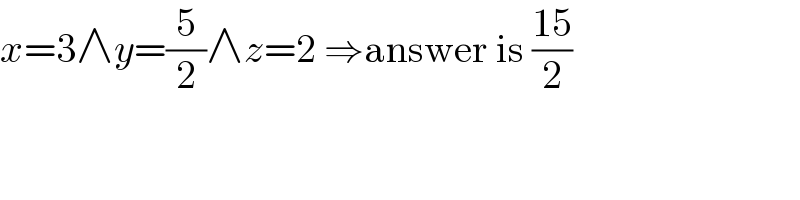
$${x}=\mathrm{3}\wedge{y}=\frac{\mathrm{5}}{\mathrm{2}}\wedge{z}=\mathrm{2}\:\Rightarrow\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{15}}{\mathrm{2}} \\ $$
Commented by tri26112004 last updated on 01/Jul/23
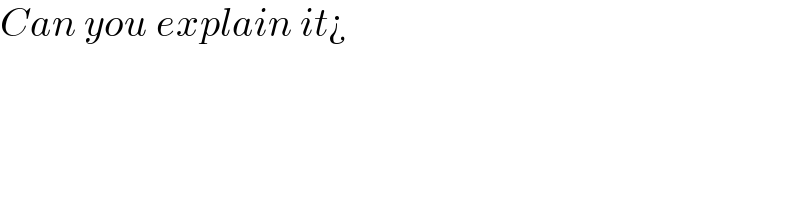
$${Can}\:{you}\:{explain}\:{it}¿ \\ $$
Answered by mr W last updated on 01/Jul/23
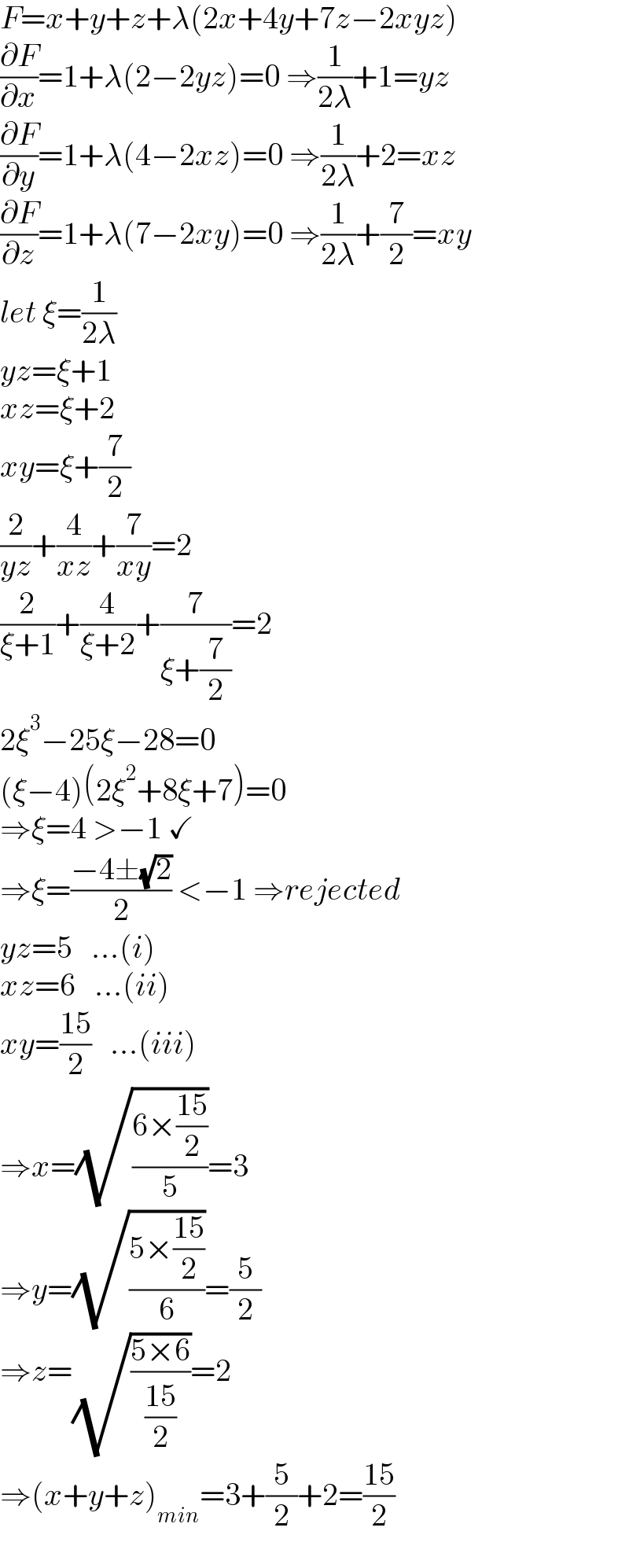
$${F}={x}+{y}+{z}+\lambda\left(\mathrm{2}{x}+\mathrm{4}{y}+\mathrm{7}{z}−\mathrm{2}{xyz}\right) \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{1}+\lambda\left(\mathrm{2}−\mathrm{2}{yz}\right)=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{1}={yz} \\ $$$$\frac{\partial{F}}{\partial{y}}=\mathrm{1}+\lambda\left(\mathrm{4}−\mathrm{2}{xz}\right)=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{2}={xz} \\ $$$$\frac{\partial{F}}{\partial{z}}=\mathrm{1}+\lambda\left(\mathrm{7}−\mathrm{2}{xy}\right)=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\lambda}+\frac{\mathrm{7}}{\mathrm{2}}={xy} \\ $$$${let}\:\xi=\frac{\mathrm{1}}{\mathrm{2}\lambda} \\ $$$${yz}=\xi+\mathrm{1} \\ $$$${xz}=\xi+\mathrm{2} \\ $$$${xy}=\xi+\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}}{{yz}}+\frac{\mathrm{4}}{{xz}}+\frac{\mathrm{7}}{{xy}}=\mathrm{2} \\ $$$$\frac{\mathrm{2}}{\xi+\mathrm{1}}+\frac{\mathrm{4}}{\xi+\mathrm{2}}+\frac{\mathrm{7}}{\xi+\frac{\mathrm{7}}{\mathrm{2}}}=\mathrm{2} \\ $$$$\mathrm{2}\xi^{\mathrm{3}} −\mathrm{25}\xi−\mathrm{28}=\mathrm{0} \\ $$$$\left(\xi−\mathrm{4}\right)\left(\mathrm{2}\xi^{\mathrm{2}} +\mathrm{8}\xi+\mathrm{7}\right)=\mathrm{0} \\ $$$$\Rightarrow\xi=\mathrm{4}\:>−\mathrm{1}\:\checkmark \\ $$$$\Rightarrow\xi=\frac{−\mathrm{4}\pm\sqrt{\mathrm{2}}}{\mathrm{2}}\:<−\mathrm{1}\:\Rightarrow{rejected} \\ $$$${yz}=\mathrm{5}\:\:\:...\left({i}\right) \\ $$$${xz}=\mathrm{6}\:\:\:...\left({ii}\right) \\ $$$${xy}=\frac{\mathrm{15}}{\mathrm{2}}\:\:\:...\left({iii}\right) \\ $$$$\Rightarrow{x}=\sqrt{\frac{\mathrm{6}×\frac{\mathrm{15}}{\mathrm{2}}}{\mathrm{5}}}=\mathrm{3} \\ $$$$\Rightarrow{y}=\sqrt{\frac{\mathrm{5}×\frac{\mathrm{15}}{\mathrm{2}}}{\mathrm{6}}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{z}=\sqrt{\frac{\mathrm{5}×\mathrm{6}}{\frac{\mathrm{15}}{\mathrm{2}}}}=\mathrm{2} \\ $$$$\Rightarrow\left({x}+{y}+{z}\right)_{{min}} =\mathrm{3}+\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{2}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$
