
Question Number 208245 by Shrodinger last updated on 08/Jun/24
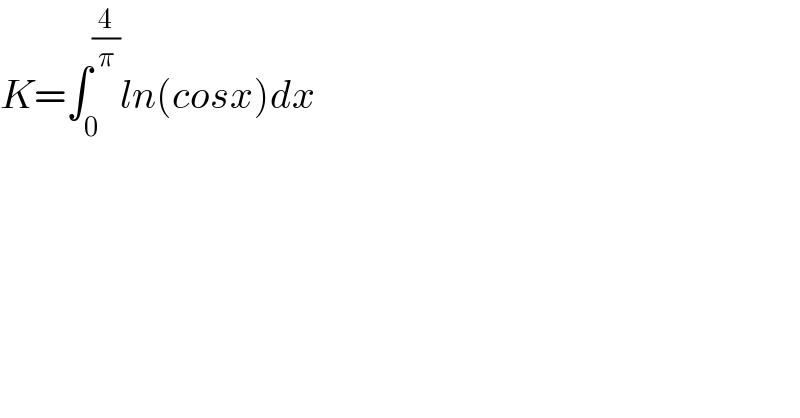
$${K}=\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{\pi}} {ln}\left({cosx}\right){dx} \\ $$
Answered by mathzup last updated on 09/Jun/24
![K=∫_0 ^(4/π) ln(((e^(ix) +e^(−ix) )/2))dx let λ=(4/π) =∫_0 ^λ ( ln(e^(ix) )+ln(1+e^(−2ix) )−ln2)dx =∫_0 ^λ ix dx+∫_0 ^λ ln(1+e^(−2ix) )dx−λln2 =i(λ^2 /2)−λln2 +∫_0 ^λ ln(1+e^(−2ix) )dx (ln(1+z)^′ =(1/(1+z))=Σ_(n=0) ^∞ (−1)^n z^n ⇒ ln(1+z)=Σ_(n=0) ^∞ (((−1)^n )/(n+1))z^(n+1) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)z^n ⇒ ∫_0 ^λ ln(1+e^(−2ix) )dx=∫_0 ^λ Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−2inx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^λ e^(−2inx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)[−(1/(2in)) e^(−2ix) ]_0 ^λ =(i/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )( e^(−2iλ) −1) =(i/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )( e^(−2iλ) −1) =−(i/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) +(i/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )(cos(2λ)−isin(2λ)) or I is real so I=−λln2+(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )sin(2λ) =−(4/π)ln2 +(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )sin((8/π)) rest to find the value of this serie ...be continued...](Q208250.png)
$${K}=\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{\pi}} {ln}\left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right){dx}\:\:\:{let}\:\lambda=\frac{\mathrm{4}}{\pi} \\ $$$$=\int_{\mathrm{0}} ^{\lambda} \left(\right. \\ $$$$\left.{ln}\left({e}^{{ix}} \right)+{ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{ix}} \right)−{ln}\mathrm{2}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\lambda} {ix}\:{dx}+\int_{\mathrm{0}} ^{\lambda} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{ix}} \right){dx}−\lambda{ln}\mathrm{2} \\ $$$$={i}\frac{\lambda^{\mathrm{2}} }{\mathrm{2}}−\lambda{ln}\mathrm{2}\:+\int_{\mathrm{0}} ^{\lambda} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{ix}} \right){dx} \\ $$$$\left({ln}\left(\mathrm{1}+{z}\right)^{'} =\frac{\mathrm{1}}{\mathrm{1}+{z}}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {z}^{{n}} \:\Rightarrow\right. \\ $$$${ln}\left(\mathrm{1}+{z}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{z}^{{n}+\mathrm{1}} \:+{c}\:\:\left({c}=\mathrm{0}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{z}^{{n}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\lambda} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{ix}} \right){dx}=\int_{\mathrm{0}} ^{\lambda} \sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−\mathrm{2}{inx}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\lambda} \:{e}^{−\mathrm{2}{inx}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left[−\frac{\mathrm{1}}{\mathrm{2}{in}}\:{e}^{−\mathrm{2}{ix}} \right]_{\mathrm{0}} ^{\lambda} \\ $$$$=\frac{{i}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\left(\:{e}^{−\mathrm{2}{i}\lambda} −\mathrm{1}\right) \\ $$$$=\frac{{i}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\left(\:{e}^{−\mathrm{2}{i}\lambda} −\mathrm{1}\right) \\ $$$$=−\frac{{i}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} } \\ $$$$+\frac{{i}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\left({cos}\left(\mathrm{2}\lambda\right)−{isin}\left(\mathrm{2}\lambda\right)\right) \\ $$$${or}\:{I}\:{is}\:{real}\:{so} \\ $$$${I}=−\lambda{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }{sin}\left(\mathrm{2}\lambda\right) \\ $$$$=−\frac{\mathrm{4}}{\pi}{ln}\mathrm{2}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }{sin}\left(\frac{\mathrm{8}}{\pi}\right) \\ $$$${rest}\:{to}\:{find}\:{the}\:{value}\:{of}\:{this}\:{serie} \\ $$$$...{be}\:{continued}... \\ $$
Commented by Shrodinger last updated on 10/Jun/24

$${thanks}\:{sir} \\ $$
