
Question Number 106883 by john santu last updated on 07/Aug/20
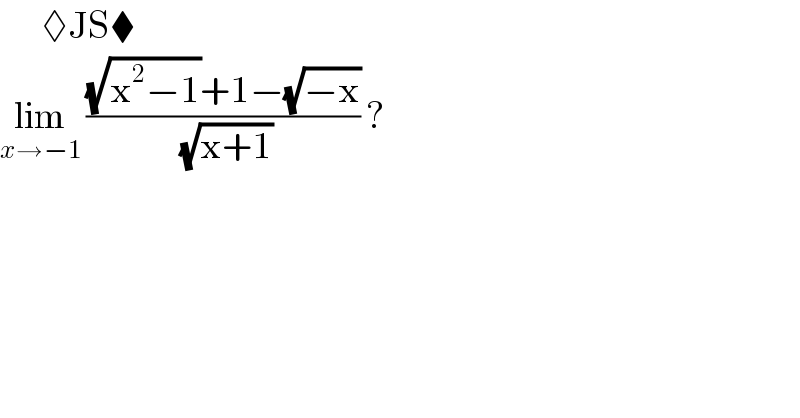
$$\:\:\:\:\:\:\:\lozenge\mathrm{JS}\blacklozenge \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}−\sqrt{−\mathrm{x}}}{\sqrt{\mathrm{x}+\mathrm{1}}}\:?\: \\ $$
Answered by bemath last updated on 07/Aug/20

$$\:\:\:\:\:\:\:@\mathrm{bemath}@ \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}+\mathrm{1}}\:\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{1}−\sqrt{−\mathrm{x}}}{\sqrt{\mathrm{x}+\mathrm{1}}}\:= \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\sqrt{\mathrm{x}−\mathrm{1}}\:+\:\frac{\mathrm{1}−\sqrt{−\mathrm{x}}}{\sqrt{\mathrm{x}+\mathrm{1}}}\:×\frac{\mathrm{1}+\sqrt{−\mathrm{x}}}{\mathrm{1}+\sqrt{−\mathrm{x}}}\:= \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\sqrt{\mathrm{x}−\mathrm{1}}\:+\:\frac{\mathrm{1}+\mathrm{x}}{\sqrt{\mathrm{x}+\mathrm{1}}\:\left(\mathrm{1}+\sqrt{−\mathrm{x}}\right)}= \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\sqrt{\mathrm{x}−\mathrm{1}}\:+\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}}{\mathrm{1}+\sqrt{−\mathrm{x}}}\right)=\mathrm{i}\sqrt{\mathrm{2}}\:?\: \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 07/Aug/20
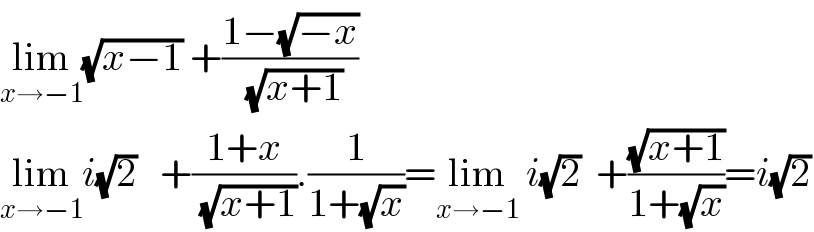
$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\sqrt{{x}−\mathrm{1}}\:+\frac{\mathrm{1}−\sqrt{−{x}}}{\sqrt{{x}+\mathrm{1}}} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{i}\sqrt{\mathrm{2}}\:\:\:+\frac{\mathrm{1}+{x}}{\sqrt{{x}+\mathrm{1}}}.\frac{\mathrm{1}}{\mathrm{1}+\sqrt{{x}}}=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:{i}\sqrt{\mathrm{2}}\:\:+\frac{\sqrt{{x}+\mathrm{1}}}{\mathrm{1}+\sqrt{{x}}}={i}\sqrt{\mathrm{2}} \\ $$
