
Question Number 129173 by bramlexs22 last updated on 13/Jan/21
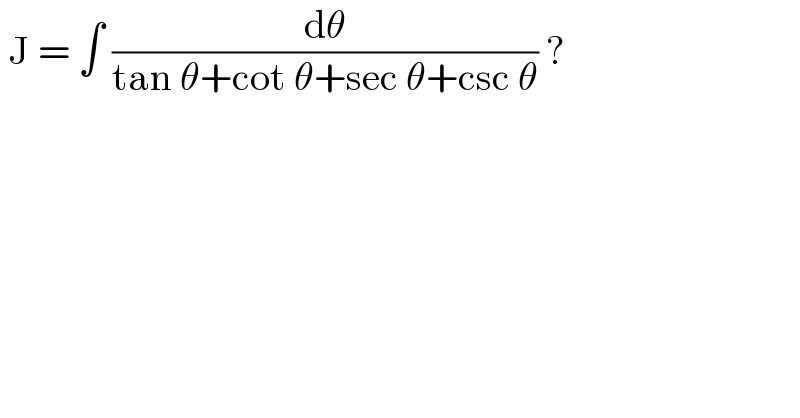
$$\:\mathrm{J}\:=\:\int\:\frac{\mathrm{d}\theta}{\mathrm{tan}\:\theta+\mathrm{cot}\:\theta+\mathrm{sec}\:\theta+\mathrm{csc}\:\theta}\:? \\ $$
Answered by liberty last updated on 13/Jan/21
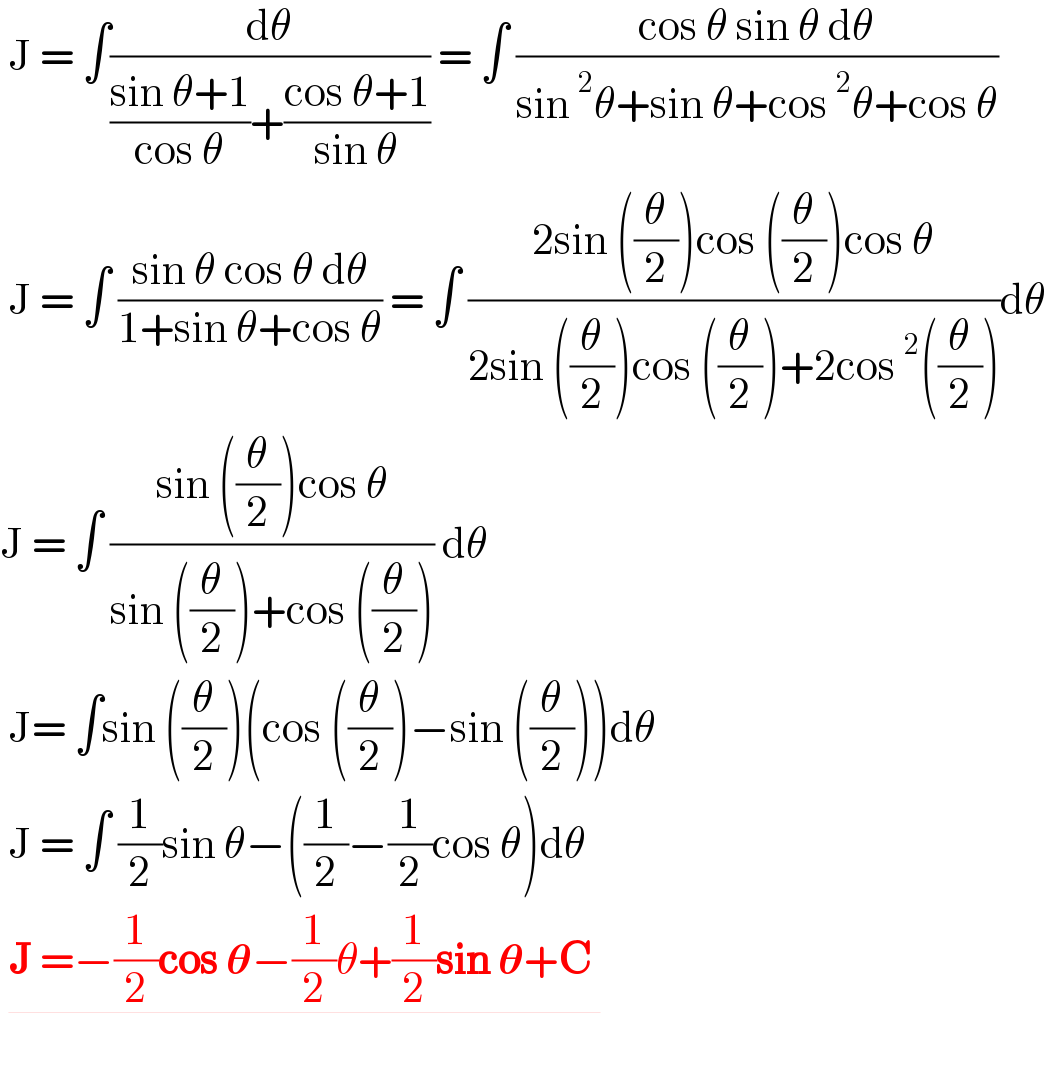
$$\:\mathrm{J}\:=\:\int\frac{\mathrm{d}\theta}{\frac{\mathrm{sin}\:\theta+\mathrm{1}}{\mathrm{cos}\:\theta}+\frac{\mathrm{cos}\:\theta+\mathrm{1}}{\mathrm{sin}\:\theta}}\:=\:\int\:\frac{\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta\:\mathrm{d}\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{sin}\:\theta+\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{cos}\:\theta} \\ $$$$\:\mathrm{J}\:=\:\int\:\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\mathrm{d}\theta}{\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{cos}\:\theta}\:=\:\int\:\frac{\mathrm{2sin}\:\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\theta}{\mathrm{2sin}\:\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}\mathrm{d}\theta \\ $$$$\mathrm{J}\:=\:\int\:\frac{\mathrm{sin}\:\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\theta}{\mathrm{sin}\:\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\theta}{\mathrm{2}}\right)}\:\mathrm{d}\theta \\ $$$$\:\mathrm{J}=\:\int\mathrm{sin}\:\left(\frac{\theta}{\mathrm{2}}\right)\left(\mathrm{cos}\:\left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{sin}\:\left(\frac{\theta}{\mathrm{2}}\right)\right)\mathrm{d}\theta \\ $$$$\:\mathrm{J}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\theta−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\theta\right)\mathrm{d}\theta \\ $$$$\:\underline{\boldsymbol{\mathrm{J}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}−\frac{\mathrm{1}}{\mathrm{2}}\theta+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}+\boldsymbol{\mathrm{C}}\:} \\ $$$$\: \\ $$
