
Question Number 205590 by Lindemann last updated on 25/Mar/24

$${J}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$
Commented by lepuissantcedricjunior last updated on 25/Mar/24
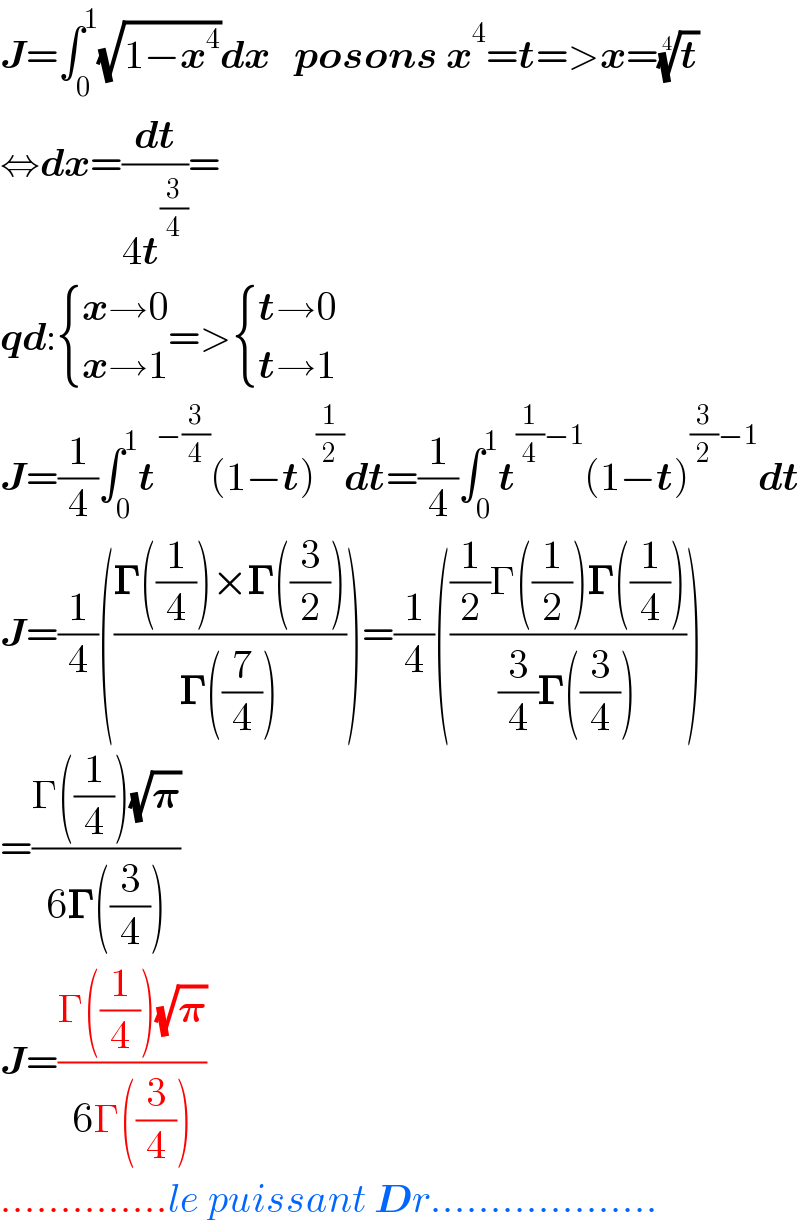
$$\boldsymbol{{J}}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{4}} }\boldsymbol{{dx}}\:\:\:\boldsymbol{{posons}}\:\boldsymbol{{x}}^{\mathrm{4}} =\boldsymbol{{t}}=>\boldsymbol{{x}}=\sqrt[{\mathrm{4}}]{\boldsymbol{{t}}} \\ $$$$\Leftrightarrow\boldsymbol{{dx}}=\frac{\boldsymbol{{dt}}}{\mathrm{4}\boldsymbol{{t}}^{\frac{\mathrm{3}}{\mathrm{4}}} }= \\ $$$$\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{x}}\rightarrow\mathrm{0}}\\{\boldsymbol{{x}}\rightarrow\mathrm{1}}\end{cases}=>\begin{cases}{\boldsymbol{{t}}\rightarrow\mathrm{0}}\\{\boldsymbol{{t}}\rightarrow\mathrm{1}}\end{cases} \\ $$$$\boldsymbol{{J}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{t}}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−\boldsymbol{{t}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dt}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{t}}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \left(\mathrm{1}−\boldsymbol{{t}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \boldsymbol{{dt}} \\ $$$$\boldsymbol{{J}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)×\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\frac{\mathrm{7}}{\mathrm{4}}\right)}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\frac{\mathrm{3}}{\mathrm{4}}\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}\right) \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\sqrt{\boldsymbol{\pi}}}{\mathrm{6}\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$\boldsymbol{{J}}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\sqrt{\boldsymbol{\pi}}}{\mathrm{6}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$..............{le}\:{puissant}\:\boldsymbol{{D}}{r}................... \\ $$
Commented by mr W last updated on 26/Mar/24
$${please}\:{post}\:{your}\:{answer}\:{to}\:{a}\:{question} \\ $$$${as}\:``{answer}'',\:{not}\:{as}\:``{comment}''!\:{thanks}! \\ $$
