Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 63428 by Rio Michael last updated on 04/Jul/19

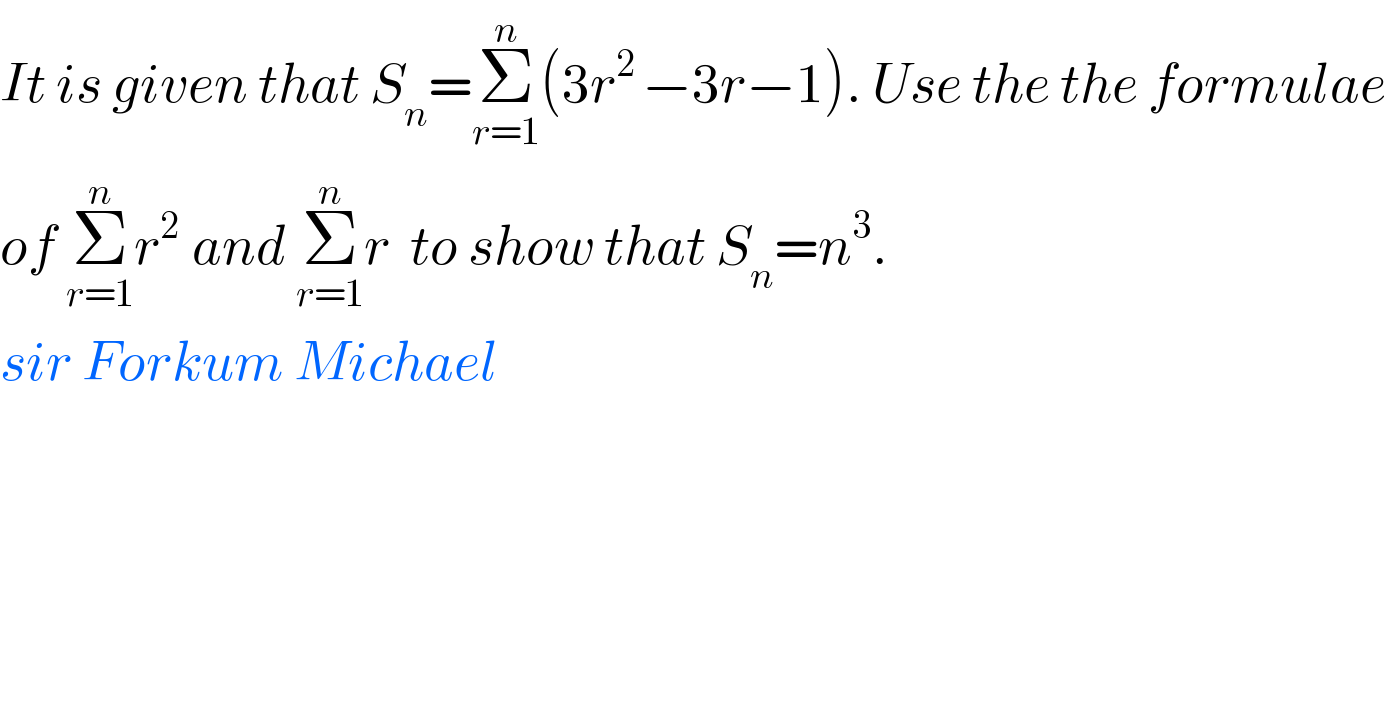
It is given that S_n =Σ_(r=1) ^n (3r^(2 ) −3r−1). Use the the formulae of Σ_(r=1) ^n r^(2 ) and Σ_(r=1) ^n r to show that S_n =n^3 . sir Forkum Michael

$${It}\:{is}\:{given}\:{that}\:{S}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{r}^{\mathrm{2}\:} −\mathrm{3}{r}−\mathrm{1}\right).\:{Use}\:{the}\:{the}\:{formulae} \\ $$$${of}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{2}\:\:} {and}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\:\:{to}\:{show}\:{that}\:{S}_{{n}} ={n}^{\mathrm{3}} . \\ $$$${sir}\:{Forkum}\:{Michael} \\ $$

Commented by Tony Lin last updated on 04/Jul/19

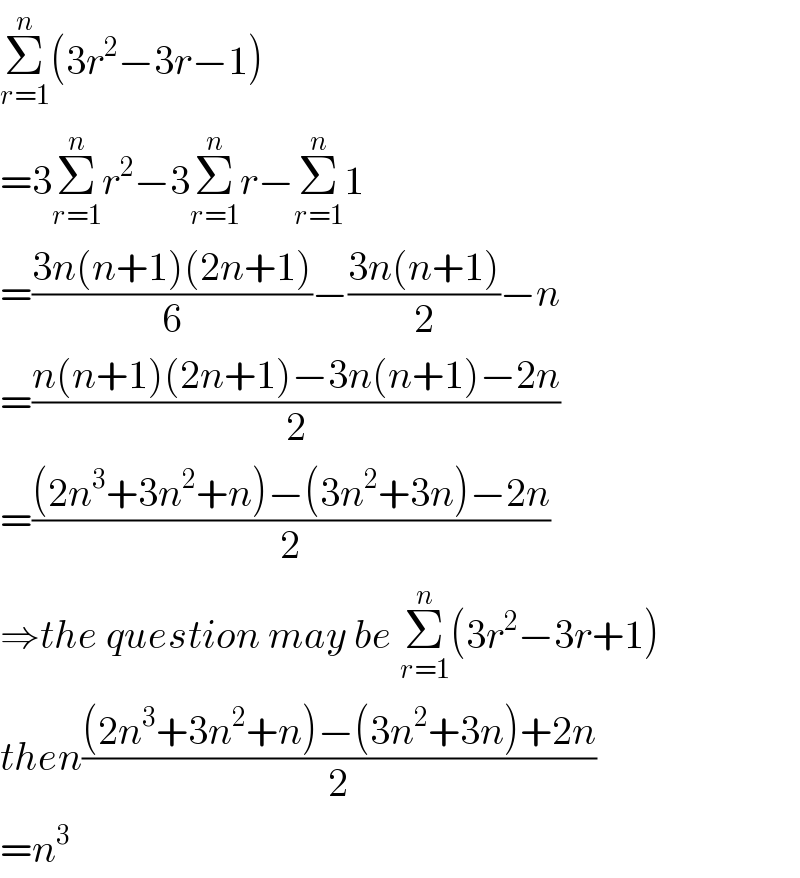
Σ_(r=1) ^n (3r^2 −3r−1) =3Σ_(r=1) ^n r^2 −3Σ_(r=1) ^n r−Σ_(r=1) ^n 1 =((3n(n+1)(2n+1))/6)−((3n(n+1))/2)−n =((n(n+1)(2n+1)−3n(n+1)−2n)/2) =(((2n^3 +3n^2 +n)−(3n^2 +3n)−2n)/2) ⇒the question may be Σ_(r=1) ^n (3r^2 −3r+1) then(((2n^3 +3n^2 +n)−(3n^2 +3n)+2n)/2) =n^3

$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{r}^{\mathrm{2}} −\mathrm{3}{r}−\mathrm{1}\right) \\ $$$$=\mathrm{3}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{2}} −\mathrm{3}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1} \\ $$$$=\frac{\mathrm{3}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}−\frac{\mathrm{3}{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−{n} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{3}{n}\left({n}+\mathrm{1}\right)−\mathrm{2}{n}}{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +{n}\right)−\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}\right)−\mathrm{2}{n}}{\mathrm{2}} \\ $$$$\Rightarrow{the}\:{question}\:{may}\:{be}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{r}^{\mathrm{2}} −\mathrm{3}{r}+\mathrm{1}\right) \\ $$$${then}\frac{\left(\mathrm{2}{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +{n}\right)−\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}\right)+\mathrm{2}{n}}{\mathrm{2}} \\ $$$$={n}^{\mathrm{3}} \\ $$

Commented by Rio Michael last updated on 04/Jul/19

correct

$${correct} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com