
Question Number 183459 by Matica last updated on 26/Dec/22
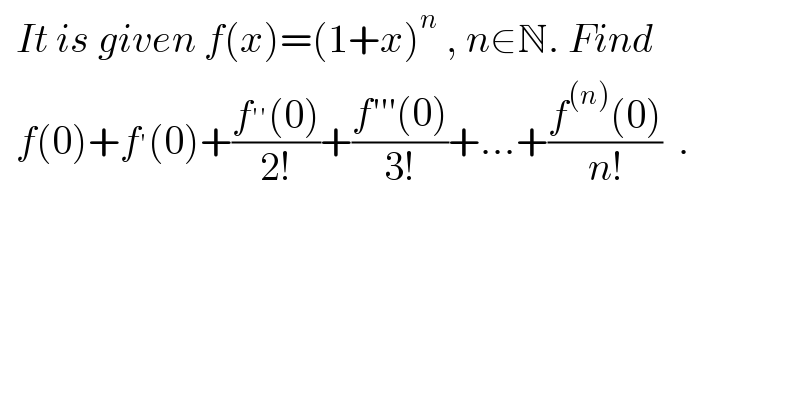
$$\:\:{It}\:{is}\:{given}\:{f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} \:,\:{n}\in\mathbb{N}.\:{Find} \\ $$$$\:\:{f}\left(\mathrm{0}\right)+{f}^{'} \left(\mathrm{0}\right)+\frac{{f}^{''} \left(\mathrm{0}\right)}{\mathrm{2}!}+\frac{{f}'''\left(\mathrm{0}\right)}{\mathrm{3}!}+...+\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:\:. \\ $$
Answered by mahdipoor last updated on 26/Dec/22
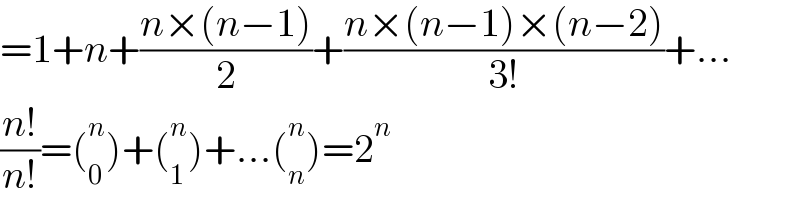
$$=\mathrm{1}+{n}+\frac{{n}×\left({n}−\mathrm{1}\right)}{\mathrm{2}}+\frac{{n}×\left({n}−\mathrm{1}\right)×\left({n}−\mathrm{2}\right)}{\mathrm{3}!}+... \\ $$$$\frac{{n}!}{{n}!}=\left(_{\mathrm{0}} ^{{n}} \right)+\left(_{\mathrm{1}} ^{{n}} \right)+...\left(_{{n}} ^{{n}} \right)=\mathrm{2}^{{n}} \\ $$
Commented by Matica last updated on 26/Dec/22
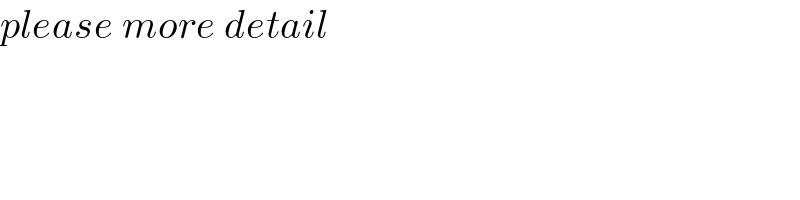
$${please}\:{more}\:{detail} \\ $$
Commented by mahdipoor last updated on 26/Dec/22
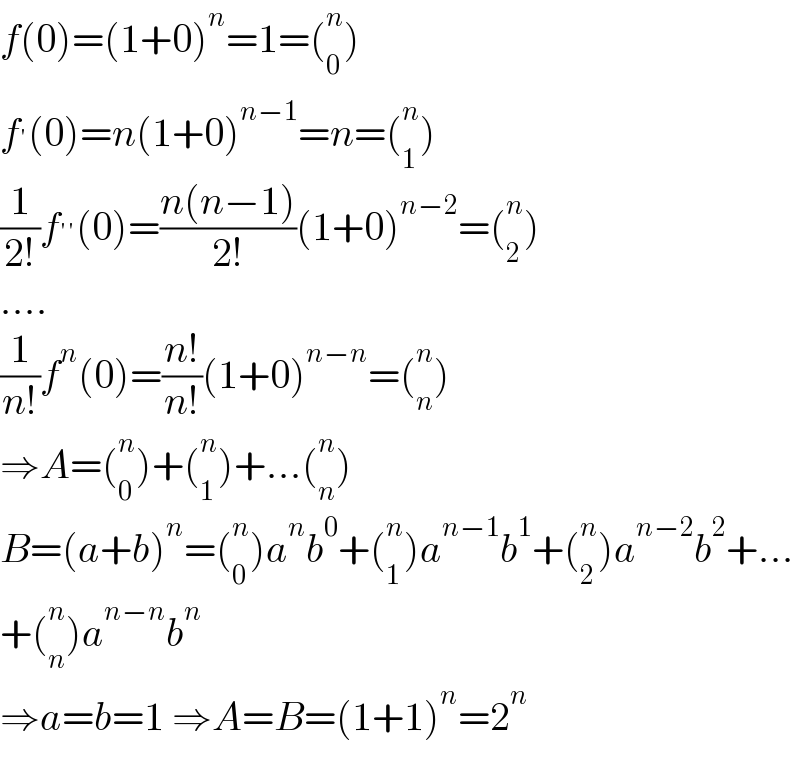
$${f}\left(\mathrm{0}\right)=\left(\mathrm{1}+\mathrm{0}\right)^{{n}} =\mathrm{1}=\left(_{\mathrm{0}} ^{{n}} \right) \\ $$$${f}^{'} \left(\mathrm{0}\right)={n}\left(\mathrm{1}+\mathrm{0}\right)^{{n}−\mathrm{1}} ={n}=\left(_{\mathrm{1}} ^{{n}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}{f}^{''} \left(\mathrm{0}\right)=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}\left(\mathrm{1}+\mathrm{0}\right)^{{n}−\mathrm{2}} =\left(_{\mathrm{2}} ^{{n}} \right) \\ $$$$.... \\ $$$$\frac{\mathrm{1}}{{n}!}{f}^{{n}} \left(\mathrm{0}\right)=\frac{{n}!}{{n}!}\left(\mathrm{1}+\mathrm{0}\right)^{{n}−{n}} =\left(_{{n}} ^{{n}} \right) \\ $$$$\Rightarrow{A}=\left(_{\mathrm{0}} ^{{n}} \right)+\left(_{\mathrm{1}} ^{{n}} \right)+...\left(_{{n}} ^{{n}} \right) \\ $$$${B}=\left({a}+{b}\right)^{{n}} =\left(_{\mathrm{0}} ^{{n}} \right){a}^{{n}} {b}^{\mathrm{0}} +\left(_{\mathrm{1}} ^{{n}} \right){a}^{{n}−\mathrm{1}} {b}^{\mathrm{1}} +\left(_{\mathrm{2}} ^{{n}} \right){a}^{{n}−\mathrm{2}} {b}^{\mathrm{2}} +... \\ $$$$+\left(_{{n}} ^{{n}} \right){a}^{{n}−{n}} {b}^{{n}} \: \\ $$$$\Rightarrow{a}={b}=\mathrm{1}\:\Rightarrow{A}={B}=\left(\mathrm{1}+\mathrm{1}\right)^{{n}} =\mathrm{2}^{{n}} \\ $$
Commented by Matica last updated on 26/Dec/22

$${Thank}\:{you}\:! \\ $$
Answered by mr W last updated on 26/Dec/22
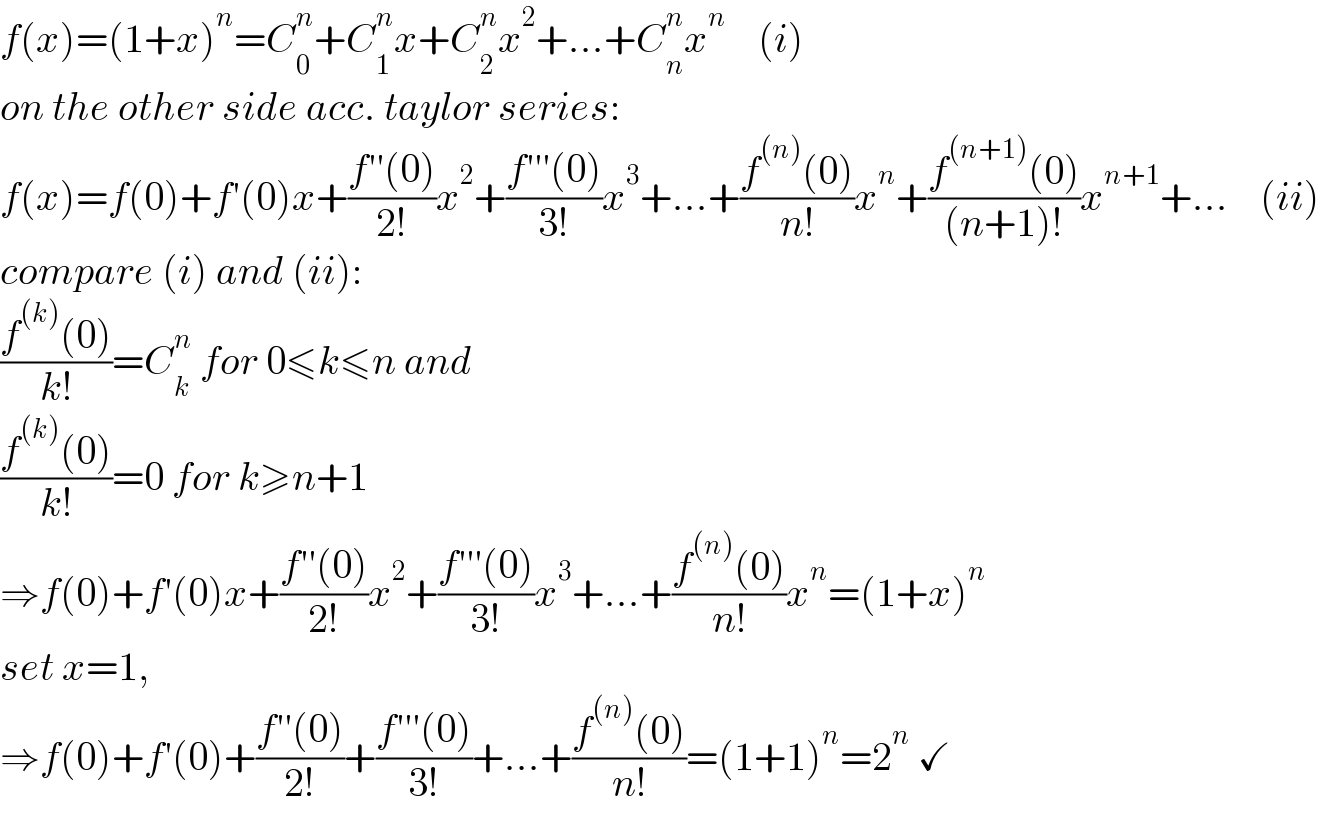
$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} ={C}_{\mathrm{0}} ^{{n}} +{C}_{\mathrm{1}} ^{{n}} {x}+{C}_{\mathrm{2}} ^{{n}} {x}^{\mathrm{2}} +...+{C}_{{n}} ^{{n}} {x}^{{n}} \:\:\:\:\left({i}\right) \\ $$$${on}\:{the}\:{other}\:{side}\:{acc}.\:{taylor}\:{series}: \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{f}'\left(\mathrm{0}\right){x}+\frac{{f}''\left(\mathrm{0}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{f}'''\left(\mathrm{0}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +...+\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} +\frac{{f}^{\left({n}+\mathrm{1}\right)} \left(\mathrm{0}\right)}{\left({n}+\mathrm{1}\right)!}{x}^{{n}+\mathrm{1}} +...\:\:\:\:\left({ii}\right) \\ $$$${compare}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\frac{{f}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}={C}_{{k}} ^{{n}} \:{for}\:\mathrm{0}\leqslant{k}\leqslant{n}\:{and} \\ $$$$\frac{{f}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}=\mathrm{0}\:{for}\:{k}\geqslant{n}+\mathrm{1} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)+{f}'\left(\mathrm{0}\right){x}+\frac{{f}''\left(\mathrm{0}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{f}'''\left(\mathrm{0}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +...+\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} =\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${set}\:{x}=\mathrm{1}, \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)+{f}'\left(\mathrm{0}\right)+\frac{{f}''\left(\mathrm{0}\right)}{\mathrm{2}!}+\frac{{f}'''\left(\mathrm{0}\right)}{\mathrm{3}!}+...+\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}=\left(\mathrm{1}+\mathrm{1}\right)^{{n}} =\mathrm{2}^{{n}} \:\checkmark \\ $$
Commented by Matica last updated on 26/Dec/22

$${Thank}\:{you}! \\ $$
