
Question Number 211122 by hardmath last updated on 28/Aug/24

$$ \\ $$Is there a special rule for divisibility of four-digit numbers by 13?
Answered by mahdipoor last updated on 28/Aug/24
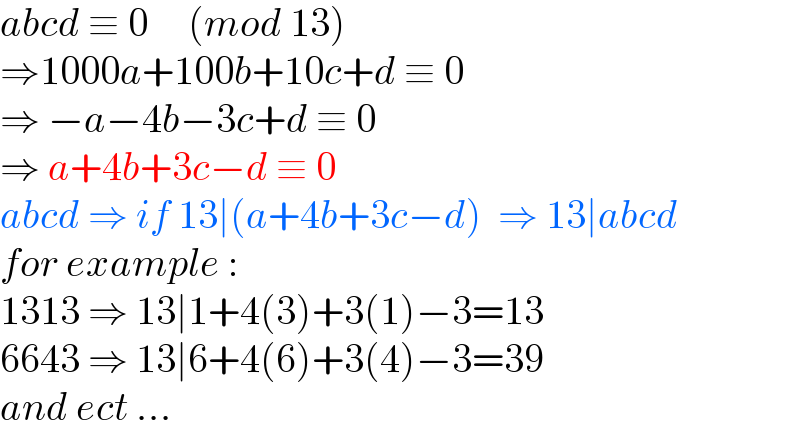
$${abcd}\:\equiv\:\mathrm{0}\:\:\:\:\:\left({mod}\:\mathrm{13}\right) \\ $$$$\Rightarrow\mathrm{1000}{a}+\mathrm{100}{b}+\mathrm{10}{c}+{d}\:\equiv\:\mathrm{0}\: \\ $$$$\Rightarrow\:−{a}−\mathrm{4}{b}−\mathrm{3}{c}+{d}\:\equiv\:\mathrm{0}\: \\ $$$$\Rightarrow\:{a}+\mathrm{4}{b}+\mathrm{3}{c}−{d}\:\equiv\:\mathrm{0}\: \\ $$$${abcd}\:\Rightarrow\:{if}\:\mathrm{13}\mid\left({a}+\mathrm{4}{b}+\mathrm{3}{c}−{d}\right)\:\:\Rightarrow\:\mathrm{13}\mid{abcd} \\ $$$${for}\:{example}\:: \\ $$$$\mathrm{1313}\:\Rightarrow\:\mathrm{13}\mid\mathrm{1}+\mathrm{4}\left(\mathrm{3}\right)+\mathrm{3}\left(\mathrm{1}\right)−\mathrm{3}=\mathrm{13}\: \\ $$$$\mathrm{6643}\:\Rightarrow\:\mathrm{13}\mid\mathrm{6}+\mathrm{4}\left(\mathrm{6}\right)+\mathrm{3}\left(\mathrm{4}\right)−\mathrm{3}=\mathrm{39} \\ $$$${and}\:{ect}\:... \\ $$
