
Question Number 209398 by SonGoku last updated on 09/Jul/24

$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{points}\:\mathrm{A}\left(\mathrm{x}_{\mathrm{1}} ,\:\mathrm{y}_{\mathrm{1}} \right)\:\mathrm{and} \\ $$$$\mathrm{B}\left(\mathrm{x}_{\mathrm{2}} ,\:\mathrm{y}_{\mathrm{2}} \right)\:\mathrm{knowing}\:\mathrm{that}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{them}\:\mathrm{is} \\ $$$$\mathrm{2}\sqrt{\mathrm{29}}? \\ $$
Answered by Frix last updated on 09/Jul/24
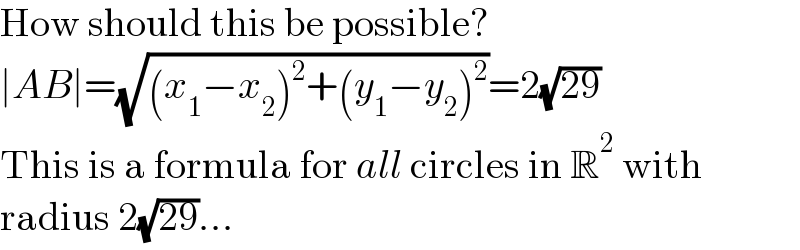
$$\mathrm{How}\:\mathrm{should}\:\mathrm{this}\:\mathrm{be}\:\mathrm{possible}? \\ $$$$\mid{AB}\mid=\sqrt{\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{29}} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{a}\:\mathrm{formula}\:\mathrm{for}\:{all}\:\mathrm{circles}\:\mathrm{in}\:\mathbb{R}^{\mathrm{2}} \:\mathrm{with} \\ $$$$\mathrm{radius}\:\mathrm{2}\sqrt{\mathrm{29}}... \\ $$
Commented by SonGoku last updated on 09/Jul/24
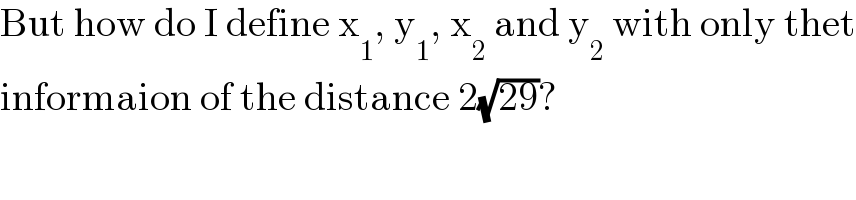
$$\mathrm{But}\:\mathrm{how}\:\mathrm{do}\:\mathrm{I}\:\mathrm{define}\:\mathrm{x}_{\mathrm{1}} ,\:\mathrm{y}_{\mathrm{1}} ,\:\mathrm{x}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{y}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{only}\:\mathrm{thet} \\ $$$$\mathrm{informaion}\:\mathrm{of}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{2}\sqrt{\mathrm{29}}? \\ $$
Commented by Frix last updated on 09/Jul/24

$$\mathrm{You}\:\mathrm{cannot}. \\ $$
