
IntegrationQuestion and Answers: Page 79
Question Number 147477 Answers: 1 Comments: 1
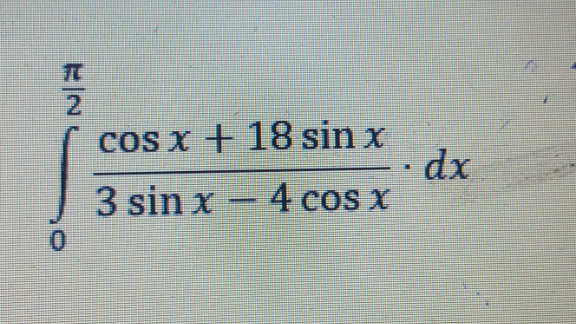
Question Number 147399 Answers: 0 Comments: 0
Question Number 147310 Answers: 1 Comments: 1
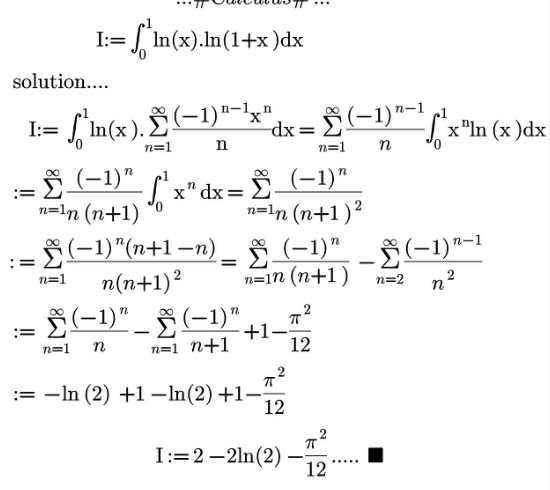
Question Number 147309 Answers: 2 Comments: 0

Question Number 147287 Answers: 2 Comments: 0
Question Number 147275 Answers: 1 Comments: 0
Question Number 147206 Answers: 0 Comments: 0
Question Number 147203 Answers: 1 Comments: 0
Question Number 147202 Answers: 0 Comments: 0
Question Number 147166 Answers: 2 Comments: 0
Question Number 147163 Answers: 0 Comments: 0
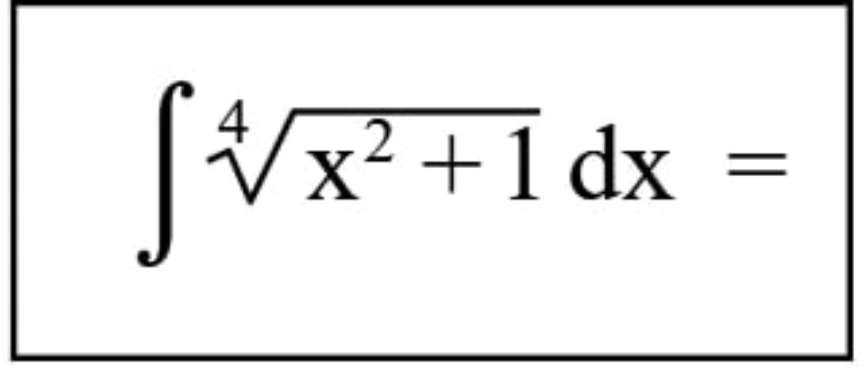
Question Number 147101 Answers: 1 Comments: 0
Question Number 147061 Answers: 2 Comments: 0
Question Number 147060 Answers: 1 Comments: 0
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{\mathrm{2}{x}} \sqrt{{tanx}}{dx} \\ $$
Question Number 147035 Answers: 2 Comments: 0
Question Number 146996 Answers: 1 Comments: 0
Question Number 146962 Answers: 1 Comments: 0

Question Number 146933 Answers: 0 Comments: 0
Question Number 146836 Answers: 0 Comments: 0
Question Number 146835 Answers: 2 Comments: 0
Question Number 146791 Answers: 1 Comments: 0
Question Number 146790 Answers: 1 Comments: 0
Question Number 146767 Answers: 1 Comments: 0
Question Number 146756 Answers: 2 Comments: 0
Question Number 146752 Answers: 1 Comments: 0
Question Number 146736 Answers: 1 Comments: 0
