Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 77

Question Number 149498 Answers: 2 Comments: 0

∫((px+q)/( (√(x^2 +r^2 ))))

$$ \\ $$$$\int\frac{{px}+{q}}{\:\sqrt{{x}^{\mathrm{2}} +{r}^{\mathrm{2}} }} \\ $$

Question Number 149329 Answers: 1 Comments: 1

Question Number 149273 Answers: 3 Comments: 0

∫_0 ^(π/4) ((e^(tan x) sin^2 x)/(cos^4 x)) dx =?

$$\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{e}^{\mathrm{tan}\:\mathrm{x}} \:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$

Question Number 149241 Answers: 2 Comments: 0

Question Number 149205 Answers: 1 Comments: 0

∫_(−∞) ^0 (t/((1−t)^2 ))dt

$$\int_{−\infty} ^{\mathrm{0}} \frac{{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt} \\ $$

Question Number 149157 Answers: 1 Comments: 0

∫_(1/2) ^2 (1/x)cosec^(101) (x−(1/x)) dx=?

$$\underset{\frac{\mathrm{1}}{\mathrm{2}}} {\overset{\mathrm{2}} {\int}}\frac{\mathrm{1}}{{x}}\mathrm{cosec}\:^{\mathrm{101}} \left({x}−\frac{\mathrm{1}}{{x}}\right)\:{dx}=? \\ $$

Question Number 149156 Answers: 0 Comments: 0

if ∫(dx/( (((1+x^2 )^(1012) (2+x^2 )^(3012) ))^(1/(2012)) ))=(α/(2β))(1−f(x))^(β/α) then find α,β,f(x)

$${if}\:\int\frac{{dx}}{\:\sqrt[{\mathrm{2012}}]{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{1012}} \left(\mathrm{2}+{x}^{\mathrm{2}} \right)^{\mathrm{3012}} }}=\frac{\alpha}{\mathrm{2}\beta}\left(\mathrm{1}−{f}\left({x}\right)\right)^{\frac{\beta}{\alpha}} \\ $$$${then}\:{find}\:\alpha,\beta,{f}\left({x}\right) \\ $$

Question Number 149113 Answers: 1 Comments: 0

∫_0 ^( π) ((cos^3 x)/(7−sin^2 x)) dx =?

$$\:\int_{\mathrm{0}} ^{\:\pi} \:\frac{\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{7}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$

Question Number 149112 Answers: 0 Comments: 2

ϕ = ∫ tan (x+(π/3))tan 3x tan (2x−(π/3)) dx =?

$$\:\varphi\:=\:\int\:\mathrm{tan}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{3}}\right)\mathrm{tan}\:\mathrm{3x}\:\mathrm{tan}\:\left(\mathrm{2x}−\frac{\pi}{\mathrm{3}}\right)\:\mathrm{dx}\:=? \\ $$

Question Number 149106 Answers: 0 Comments: 0

Question Number 149081 Answers: 1 Comments: 0

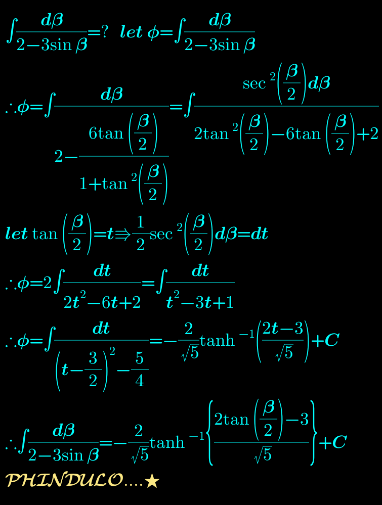
Question Number 149080 Answers: 0 Comments: 0

Question Number 149023 Answers: 1 Comments: 0

∫_0 ^(π/4) ((tsint)/(1+cos^2 t))dt=∫_0 ^(π/4) ((tcost)/(1+sin^2 t))dt true or false ??

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tsint}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}=\overset{\frac{\pi}{\mathrm{4}}} {\int}_{\mathrm{0}} \frac{{tcost}}{\mathrm{1}+{sin}^{\mathrm{2}} {t}}{dt} \\ $$$${true}\:{or}\:{false}\:?? \\ $$

Question Number 148981 Answers: 0 Comments: 0

∫_((√2)/2) ^1 ((arc cosu)/(u^2 +1))du

$$\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{arc}\:{cosu}}{{u}^{\mathrm{2}} +\mathrm{1}}{du} \\ $$

Question Number 148942 Answers: 0 Comments: 0

M=∫_0 ^(+∞) ((x^(2n) lnx)/(x^2 +1))dx

$${M}=\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{\mathrm{2}{n}} {lnx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$ \\ $$

Question Number 148905 Answers: 1 Comments: 0

Question Number 148895 Answers: 0 Comments: 2

Question Number 148856 Answers: 0 Comments: 3

pls solve

$${pls}\:{solve} \\ $$

Question Number 148854 Answers: 0 Comments: 0

∫(√((A∙B∙(√(x^2 +y^2 )))/((x^2 +y^2 )B^2 +C)))dx= ? A,B,C=const.

$$\int\sqrt{\frac{{A}\centerdot{B}\centerdot\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){B}^{\mathrm{2}} +{C}}}{dx}=\:\:? \\ $$$${A},{B},{C}={const}. \\ $$

Question Number 148815 Answers: 0 Comments: 0

calculate ∫_0 ^∞ (x^n /((x^(2n) +1)^2 ))dx (n≥2 integr)

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{n}} }{\left(\mathrm{x}^{\mathrm{2n}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\:\:\:\left(\mathrm{n}\geqslant\mathrm{2}\:\:\mathrm{integr}\right) \\ $$

Question Number 148809 Answers: 1 Comments: 0

Σ_(i=0) ^∞ [(−0.5x^2 )i/i!] integrate

$$\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\left(−\mathrm{0}.\mathrm{5x}^{\mathrm{2}} \right)\mathrm{i}/\mathrm{i}!\right]\:\mathrm{integrate} \\ $$

Question Number 148816 Answers: 1 Comments: 0

∫_0 ^∞ x^m e^(ix^n ) dx=??

$$\int_{\mathrm{0}} ^{\infty} {x}^{{m}} {e}^{{ix}^{{n}} } {dx}=?? \\ $$

Question Number 150871 Answers: 1 Comments: 0

Find all the real solutions of cos x+cos^5 x+cos 7x=3

$$\:\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{of}\:\mathrm{cos}\:\mathrm{x}+\mathrm{cos}\:^{\mathrm{5}} \mathrm{x}+\mathrm{cos}\:\mathrm{7x}=\mathrm{3} \\ $$

Question Number 148720 Answers: 4 Comments: 0

Find the Talor series of ((ln(1−x))/((1−x)^2 )) at x=0.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{Talor}\:\mathrm{series}\:\mathrm{of}\:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{at}\:\mathrm{x}=\mathrm{0}. \\ $$

Question Number 148570 Answers: 2 Comments: 0

calculate ∫_0 ^∞ ((logx)/(x^2 +x+1))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$

Question Number 148567 Answers: 1 Comments: 0

find ∫_0 ^∞ ((x^2 logx)/((x^2 +1)^3 ))dx

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$

Pg 72 Pg 73 Pg 74 Pg 75 Pg 76 Pg 77 Pg 78 Pg 79 Pg 80 Pg 81

Contact: info@tinkutara.com