Question and Answers Forum

IntegrationQuestion and Answers: Page 59

Question Number 163414 Answers: 1 Comments: 0

∫(dx/( (√(cosx sin^3 x))+(√(sinx cos^3 x))))

$$\int\frac{\boldsymbol{{dx}}}{\:\sqrt{\boldsymbol{{cosx}}\:\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{x}}}+\sqrt{\boldsymbol{{sinx}}\:\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}}} \\ $$

Question Number 163357 Answers: 1 Comments: 0

∫_0 ^( 1) ln(3x−3x^( 2) + x^( 3) )= ?

$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\mathrm{3}{x}−\mathrm{3}{x}^{\:\mathrm{2}} +\:{x}^{\:\mathrm{3}} \right)=\:? \\ $$$$ \\ $$

Question Number 163349 Answers: 1 Comments: 0

Question Number 163197 Answers: 0 Comments: 1

Question Number 163212 Answers: 1 Comments: 3

Question Number 163158 Answers: 1 Comments: 0

prove that ∫_0 ^( (π/4)) (( sin(x)+cos(x))/( (√(1+sin(x)cos(x))))) dx= (√2) .cot^( −1) ((√2) ) −−−−−

$$ \\ $$$$\:\:\:\:\:{prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\:{sin}\left({x}\right)+{cos}\left({x}\right)}{\:\sqrt{\mathrm{1}+{sin}\left({x}\right){cos}\left({x}\right)}}\:{dx}=\:\sqrt{\mathrm{2}}\:.{cot}^{\:−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:\right) \\ $$$$\:\:\:−−−−− \\ $$

Question Number 163119 Answers: 2 Comments: 0

f ′(x)= f(x)+∫_0 ^1 f(x)dx f(0)=1 ⇒f(x)=?

$$\:\:{f}\:'\left({x}\right)=\:{f}\left({x}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\: \\ $$$$\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow{f}\left({x}\right)=? \\ $$

Question Number 163114 Answers: 1 Comments: 0

∫(((cos5x+cos4x)/(1+2cos3x))) dx

$$\int\left(\frac{\boldsymbol{\mathrm{cos}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\mathrm{2}\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}}\right)\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\: \\ $$

Question Number 163109 Answers: 1 Comments: 0

find the value of ∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^n ))dx (n fromN and n≥1)

$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx}\:\:\:\:\:\left(\mathrm{n}\:\mathrm{fromN}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{1}\right) \\ $$

Question Number 163072 Answers: 1 Comments: 0

∫((sinx+sin3x+sin5x+sin7x)/(cosx+cos3x+cos5x+cos7x)) dx

$$\int\frac{\boldsymbol{\mathrm{sinx}}+\boldsymbol{\mathrm{sin}}\mathrm{3}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{sin}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{sin}}\mathrm{7}\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{cosx}}+\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{7}\boldsymbol{\mathrm{x}}}\:\boldsymbol{\mathrm{dx}} \\ $$

Question Number 163008 Answers: 2 Comments: 0

Calculate ∫ (((2−4sin x cos x)(1+sin 2x))/(sin^4 2x+64 cos^4 2x)) dx

$$\:{Calculate}\: \\ $$$$\:\:\:\int\:\frac{\left(\mathrm{2}−\mathrm{4sin}\:{x}\:\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}}\:{dx}\: \\ $$$$ \\ $$

Question Number 162894 Answers: 1 Comments: 0

Question Number 162893 Answers: 2 Comments: 0

Ω=∫_0 ^( 1) ((( x^ )/(ln^ ( 1−x ))))^( 2) dx=^? ln ((( 27)/(16)) ) −−−−

$$ \\ $$$$\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\:{x}^{\:} }{\mathrm{ln}^{\:} \left(\:\mathrm{1}−{x}\:\right)}\right)^{\:\mathrm{2}} {dx}\overset{?} {=}\:\mathrm{ln}\:\left(\frac{\:\mathrm{27}}{\mathrm{16}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:−−−− \\ $$$$ \\ $$

Question Number 162864 Answers: 2 Comments: 0

Question Number 162811 Answers: 1 Comments: 0

I = ∫_0 ^( ∞) (( tan^( −1) (x ))/(( 1+x^( 2) )^( 2) )) dx = ? −−−−−−−−−−

$$ \\ $$$$\:\:\:\:\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{tan}^{\:−\mathrm{1}} \:\left({x}\:\right)}{\left(\:\mathrm{1}+{x}^{\:\mathrm{2}} \:\right)^{\:\mathrm{2}} }\:{dx}\:=\:? \\ $$$$\:\:\:\:\:\:−−−−−−−−−− \\ $$

Question Number 162702 Answers: 0 Comments: 0

∫e^(−4x) tg(x)ln∣cos(x)∣dx=?

$$\int\boldsymbol{{e}}^{−\mathrm{4}\boldsymbol{{x}}} \boldsymbol{{tg}}\left(\boldsymbol{{x}}\right)\boldsymbol{{ln}}\mid\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\mid\boldsymbol{{dx}}=? \\ $$

Question Number 162604 Answers: 1 Comments: 0

I=∫_0 ^(π/4) xtg(x)dx=?

$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \boldsymbol{{xtg}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}=? \\ $$

Question Number 162575 Answers: 2 Comments: 0

∫_0 ^π (x^2 /(1+sinx))dx

$$\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$

Question Number 162535 Answers: 2 Comments: 3

prove that Ω = ∫_0 ^( ∞) (( ln ((1/x) ))/( x^( 4) + 17x^( 2) + 16)) dx=^? (π/(60)) ln(2)

$$ \\ $$$$\:\:\:\:\:\mathrm{prove}\:\mathrm{that} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\:\right)}{\:{x}^{\:\mathrm{4}} \:+\:\mathrm{17}{x}^{\:\mathrm{2}} \:+\:\mathrm{16}}\:{dx}\overset{?} {=}\:\frac{\pi}{\mathrm{60}}\:\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Question Number 162525 Answers: 2 Comments: 0

∫_0 ^∞ ((√x)/((x^2 +4x+4)))=?

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\sqrt{{x}}}{\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right)}=? \\ $$

Question Number 162513 Answers: 2 Comments: 0

∫_0 ^( ∞) ((log(x))/((x+1)(x+9)))

$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{log}\left(\mathrm{x}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{9}\right)} \\ $$

Question Number 162512 Answers: 0 Comments: 1

solve ∫(√(cosec^2 x−2)) dx

$${solve}\:\int\sqrt{{cosec}^{\mathrm{2}} {x}−\mathrm{2}}\:{dx} \\ $$

Question Number 162471 Answers: 2 Comments: 0

[reposted] find ∫_( 0) ^( (𝛑/2)) sin^8 (x)dx + ∫_( 0) ^( 1) sin^(-1) ((x)^(1/8) ) dx=?

$$\left[{reposted}\right] \\ $$$${find}\:\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\:\mathrm{sin}^{\mathrm{8}} \left(\mathrm{x}\right){dx}\:+\:\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{sin}^{-\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{\mathrm{x}}\right)\:{dx}=? \\ $$

Question Number 162374 Answers: 0 Comments: 2

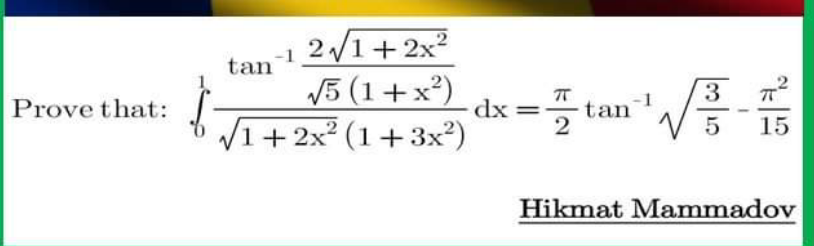
Question Number 162365 Answers: 0 Comments: 0

∫_0 ^1 ∫_0 ^1 ∫_0 ^1 ln^2 (x+y+z)dxdydz=?

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{ln}^{\mathrm{2}} \left({x}+{y}+{z}\right){dxdydz}=? \\ $$

Question Number 162348 Answers: 1 Comments: 4

Pg 54 Pg 55 Pg 56 Pg 57 Pg 58 Pg 59 Pg 60 Pg 61 Pg 62 Pg 63

Contact: info@tinkutara.com