Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 51

Question Number 169049 Answers: 1 Comments: 0

∫x^2 e^(x^2 /2) Mastermind

$$\int{x}^{\mathrm{2}} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 169048 Answers: 0 Comments: 0

find ∫_0 ^∞ ((lnx)/(x^2 −x+2))dx

$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx} \\ $$

Question Number 169042 Answers: 0 Comments: 0

Question Number 169000 Answers: 1 Comments: 0

Question Number 168978 Answers: 1 Comments: 0

Evaluate (a) ∫((t−2)/(t−3(√(2t−4)) +2)) dt (b) ∫((3z)/((1−4z−2z^2 )^2 )) dz

$$\mathrm{Evaluate}\: \\ $$$$\left(\mathrm{a}\right)\:\int\frac{{t}−\mathrm{2}}{{t}−\mathrm{3}\sqrt{\mathrm{2}{t}−\mathrm{4}}\:+\mathrm{2}}\:{dt}\: \\ $$$$\left(\mathrm{b}\right)\:\int\frac{\mathrm{3}{z}}{\left(\mathrm{1}−\mathrm{4}{z}−\mathrm{2}{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dz} \\ $$

Question Number 168898 Answers: 1 Comments: 0

Question Number 168894 Answers: 1 Comments: 1

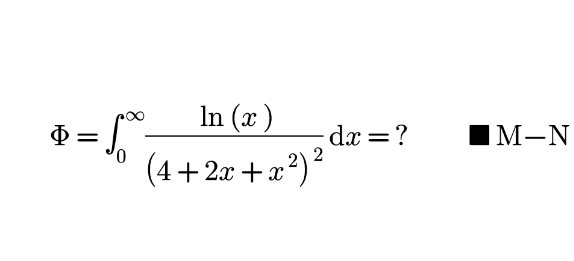
Question Number 168874 Answers: 0 Comments: 0

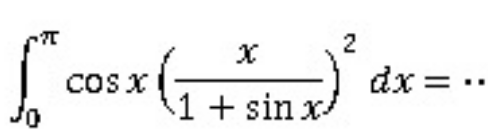
Question Number 168873 Answers: 0 Comments: 0

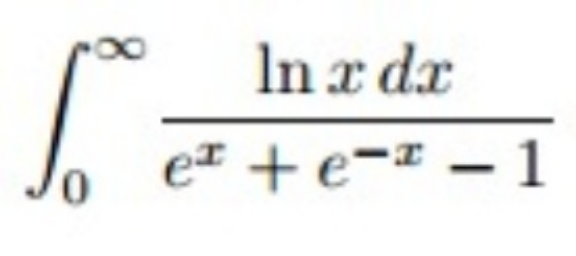
Question Number 168872 Answers: 0 Comments: 2

E=∫^π _0 [((a^2 σ sin θ)/(2ε(√(a^2 −x^2 −2ax cosθ))))]dθ If a>x show that E = ((a^2 σ)/(εx))

$${E}=\underset{\mathrm{0}} {\int}^{\pi} \left[\frac{{a}^{\mathrm{2}} \sigma\:\mathrm{sin}\:\theta}{\mathrm{2}\epsilon\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{2}{ax}\:\mathrm{cos}\theta}}\right]{d}\theta \\ $$$$\mathrm{If}\:{a}>{x}\:\mathrm{show}\:\mathrm{that}\:{E}\:=\:\frac{{a}^{\mathrm{2}} \sigma}{\epsilon{x}} \\ $$

Question Number 168860 Answers: 0 Comments: 0

Question Number 168857 Answers: 3 Comments: 0

Question Number 168852 Answers: 0 Comments: 3

Question Number 168828 Answers: 0 Comments: 1

∫_0 ^(π/2) cos^(−1) ((1/(1+2cos x)))dx

$$ \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2cos}\:{x}}\right){dx} \\ $$

Question Number 168812 Answers: 0 Comments: 0

∫_0 ^π (sin x)^(cos x) dx

$$\int_{\mathrm{0}} ^{\pi} \left(\mathrm{sin}\:{x}\right)^{\mathrm{cos}\:{x}} {dx} \\ $$

Question Number 168772 Answers: 1 Comments: 1

Question Number 168771 Answers: 0 Comments: 0

Question Number 168762 Answers: 0 Comments: 2

Question Number 168745 Answers: 1 Comments: 1

∫(1/(x+(√(x−1)))) dx = ??

$$\int\frac{\mathrm{1}}{{x}+\sqrt{{x}−\mathrm{1}}}\:{dx}\:=\:?? \\ $$

Question Number 168743 Answers: 1 Comments: 1

∫_0 ^∞ ((√t)/(1+t^2 ))dt FAILED TO CALCULATE

$$\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{FAILED}\:\mathrm{TO}\:\mathrm{CALCULATE} \\ $$$$ \\ $$

Question Number 168732 Answers: 2 Comments: 0

Question Number 168707 Answers: 1 Comments: 1

Question Number 168677 Answers: 2 Comments: 1

Question Number 168662 Answers: 0 Comments: 0

∫sin^3 (x)cos^4 (5x)dx=?

$$\int{sin}^{\mathrm{3}} \left({x}\right){cos}^{\mathrm{4}} \left(\mathrm{5}{x}\right){dx}=? \\ $$

Question Number 168649 Answers: 0 Comments: 3

Help!!!

$$\boldsymbol{{Help}}!!! \\ $$

Question Number 168652 Answers: 0 Comments: 0

Pg 46 Pg 47 Pg 48 Pg 49 Pg 50 Pg 51 Pg 52 Pg 53 Pg 54 Pg 55

Terms of Service

Contact: info@tinkutara.com