
IntegrationQuestion and Answers: Page 302
Question Number 34827 Answers: 1 Comments: 5
Question Number 34771 Answers: 0 Comments: 1
Question Number 34720 Answers: 0 Comments: 0
Question Number 34717 Answers: 0 Comments: 1
Question Number 34716 Answers: 0 Comments: 1
Question Number 34715 Answers: 0 Comments: 0
Question Number 34714 Answers: 0 Comments: 1
Question Number 34713 Answers: 0 Comments: 1
Question Number 34675 Answers: 0 Comments: 0
Question Number 34674 Answers: 0 Comments: 0
Question Number 34662 Answers: 0 Comments: 0
Question Number 34661 Answers: 0 Comments: 0
Question Number 34635 Answers: 2 Comments: 4
Question Number 34633 Answers: 0 Comments: 0
Question Number 34593 Answers: 0 Comments: 0
Question Number 34562 Answers: 1 Comments: 1
Question Number 34561 Answers: 0 Comments: 1
Question Number 34985 Answers: 1 Comments: 0
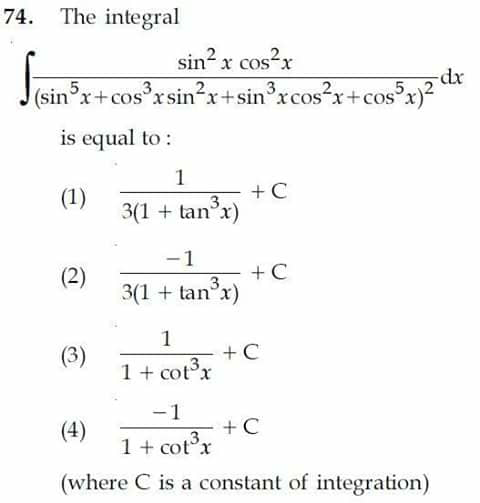
Question Number 34421 Answers: 0 Comments: 1
Question Number 34320 Answers: 0 Comments: 2
Question Number 34316 Answers: 0 Comments: 0
Question Number 34315 Answers: 0 Comments: 2
Question Number 34314 Answers: 0 Comments: 1
Question Number 34312 Answers: 0 Comments: 1
Question Number 34308 Answers: 0 Comments: 0
Question Number 34298 Answers: 0 Comments: 2
Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304 Pg 305 Pg 306
