Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 300

Question Number 35045 Answers: 0 Comments: 0

find f(x)=∫_0 ^∞ ((arctan(xt))/(1+t^2 ))dt .

$${find}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:. \\ $$

Question Number 35044 Answers: 1 Comments: 1

1)find ∫ (√(1+t^2 )) dt 2) calculate ∫_1 ^(√3) (√(1+t^2 )) dt

$$\left.\mathrm{1}\right){find}\:\int\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{dt} \\ $$

Question Number 35043 Answers: 1 Comments: 0

let t>0 and F(t) =∫_0 ^∞ ((sin(x^2 ) e^(−tx^2 ) )/x^2 )dx calculate (dF/dt)(t).

$${let}\:{t}>\mathrm{0}\:{and}\:{F}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)\:{e}^{−{tx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} }{dx} \\ $$$${calculate}\:\frac{{dF}}{{dt}}\left({t}\right). \\ $$

Question Number 35018 Answers: 1 Comments: 0

∫∫∫((dxdydz)/((x+y+z+1)^3 )) bounded by the coordinate planes and the plane x+y+z=1 .

$$\int\int\int\frac{{dxdydz}}{\left({x}+{y}+{z}+\mathrm{1}\right)^{\mathrm{3}} }\:\:\:{bounded}\:{by}\:{the} \\ $$$${coordinate}\:{planes}\:{and}\:{the}\:{plane} \\ $$$${x}+{y}+{z}=\mathrm{1}\:. \\ $$

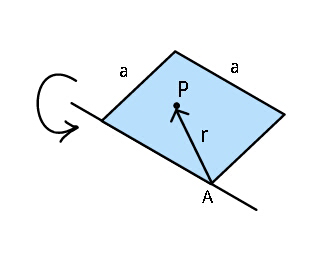
Question Number 35015 Answers: 2 Comments: 0

∫(x^2 /((1+x^3 )^2 ))dx

$$\int\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$

Question Number 34992 Answers: 1 Comments: 1

∫_0 ^π ((cos(x))/(1+2sin(2x)))dx

$$\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{cos}\left({x}\right)}{\mathrm{1}+\mathrm{2sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$

Question Number 34956 Answers: 3 Comments: 2

Question Number 34911 Answers: 1 Comments: 1

find ∫_2 ^3 ((2x^2 +3)/((x−1)^2 (x^2 +1))) dx

$${find}\:\:\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx} \\ $$

Question Number 34910 Answers: 0 Comments: 1

find J_(n,p) =∫_0 ^∞ x^n e^(−(x^2 /p)) dx with p>0 and n integr

$${find}\:{J}_{{n},{p}} \:=\int_{\mathrm{0}} ^{\infty} \:\:{x}^{{n}} \:\:{e}^{−\frac{{x}^{\mathrm{2}} }{{p}}} \:\:{dx}\:\:{with}\:{p}>\mathrm{0}\:{and}\:{n}\:{integr} \\ $$

Question Number 34901 Answers: 0 Comments: 3

∫_(−π/2) ^(+π/2) (√(cos^(2n−1) x−cos^(2n+1) x))dx =[−((2cos^((2n+1)/2) x)/(2n+1))]_(−π/2) ^(+π/2) =0? What is the mistake in above? ∫_(−π/2) ^(+π/2) (√(cos^(2n−1) x−cos^(2n+1) x))dx =2∫_0 ^(π/2) (√(cos^(2n−1) x−cos^(2n+1) x))dx =(4/(2n+1)) (this is correct answer)

$$\int_{−\pi/\mathrm{2}} ^{+\pi/\mathrm{2}} \sqrt{\mathrm{cos}^{\mathrm{2}{n}−\mathrm{1}} {x}−\mathrm{cos}^{\mathrm{2}{n}+\mathrm{1}} {x}}{dx} \\ $$$$=\left[−\frac{\mathrm{2cos}^{\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}} {x}}{\mathrm{2}{n}+\mathrm{1}}\right]_{−\pi/\mathrm{2}} ^{+\pi/\mathrm{2}} =\mathrm{0}? \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{above}? \\ $$$$\int_{−\pi/\mathrm{2}} ^{+\pi/\mathrm{2}} \sqrt{\mathrm{cos}^{\mathrm{2}{n}−\mathrm{1}} {x}−\mathrm{cos}^{\mathrm{2}{n}+\mathrm{1}} {x}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \sqrt{\mathrm{cos}^{\mathrm{2}{n}−\mathrm{1}} {x}−\mathrm{cos}^{\mathrm{2}{n}+\mathrm{1}} {x}}{dx} \\ $$$$=\frac{\mathrm{4}}{\mathrm{2}{n}+\mathrm{1}}\:\left(\mathrm{this}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{answer}\right) \\ $$

Question Number 34866 Answers: 0 Comments: 0

find f(x)=∫_0 ^∞ ((arctan(x(t +(1/t))))/(1+t^2 ))dt

$${find}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}\left({t}\:+\frac{\mathrm{1}}{{t}}\right)\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\: \\ $$

Question Number 34862 Answers: 2 Comments: 8

find the value of f(x) = ∫_0 ^π ((cosx)/(1+2sin(2x)))dx

$${find}\:{the}\:{value}\:{of} \\ $$$${f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$

Question Number 34827 Answers: 1 Comments: 5

Find ∫ Sin^6 x dx

$$\boldsymbol{{Find}}\:\int\:\boldsymbol{{Sin}}^{\mathrm{6}} \boldsymbol{{x}}\:\boldsymbol{{dx}} \\ $$$$ \\ $$

Question Number 34771 Answers: 0 Comments: 1

let A(x)= ∫_0 ^1 ln(1+ix^2 )dx find a simple form of f(x) (x∈R)

$${let}\:{A}\left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{ix}^{\mathrm{2}} \right){dx} \\ $$$${find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({x}\right)\:\:\:\:\left({x}\in{R}\right) \\ $$

Question Number 34720 Answers: 0 Comments: 0

let B(p,q) = ∫_0 ^1 x^(p−1) (1−x)^(q−1) dx calculate B((1/3), (1/3)) 2) calculate B((1/2) ,(2/3)) .

$${let}\:{B}\left({p},{q}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{p}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{q}−\mathrm{1}} {dx} \\ $$$${calculate}\:{B}\left(\frac{\mathrm{1}}{\mathrm{3}},\:\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{B}\left(\frac{\mathrm{1}}{\mathrm{2}}\:,\frac{\mathrm{2}}{\mathrm{3}}\right)\:. \\ $$

Question Number 34717 Answers: 0 Comments: 1

let I_n = ∫∫_([(1/n),n]^2 ) (((√(xy)) dxdy)/(2 +x^2 +y^2 )) find lim I_n when n→+∞.

$${let}\:{I}_{{n}} =\:\int\int_{\left[\frac{\mathrm{1}}{{n}},{n}\right]^{\mathrm{2}} } \:\:\:\:\:\frac{\sqrt{{xy}}\:{dxdy}}{\mathrm{2}\:+{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$$${find}\:{lim}\:{I}_{{n}} \:{when}\:{n}\rightarrow+\infty. \\ $$

Question Number 34716 Answers: 0 Comments: 1

calculate ∫∫_w x(√(x^2 +y^2 )) dxdy w ={(x,y)/ x^2 +y^2 ≤3 }

$${calculate}\:\int\int_{{w}} {x}\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:\:{dxdy} \\ $$$${w}\:=\left\{\left({x},{y}\right)/\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{3}\:\right\}\: \\ $$

Question Number 34715 Answers: 0 Comments: 0

calculate ∫∫_(0≤x≤y≤1) ((dxdy)/((x^2 +1)(y^2 +3))) .

$${calculate}\:\int\int_{\mathrm{0}\leqslant{x}\leqslant{y}\leqslant\mathrm{1}} \:\:\:\frac{{dxdy}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({y}^{\mathrm{2}} \:+\mathrm{3}\right)}\:. \\ $$

Question Number 34714 Answers: 0 Comments: 1

calculate ∫∫_(x^2 +2y^2 ≤1) (x^2 −y^2 )dxdy

$${calculate}\:\int\int_{{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \:\leqslant\mathrm{1}} \left({x}^{\mathrm{2}} \:−{y}^{\mathrm{2}} \right){dxdy} \\ $$

Question Number 34713 Answers: 0 Comments: 1

let a>0 calculate ∫∫_(x^2 +y^2 ≤3) (1/(2 +x^2 +y^2 ))dxdy.

$${let}\:{a}>\mathrm{0}\:\:{calculate}\:\int\int_{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{3}} \:\frac{\mathrm{1}}{\mathrm{2}\:+{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}. \\ $$

Question Number 34675 Answers: 0 Comments: 0

provethat e = Σ_(k=0) ^n (1/(k!)) +∫_0 ^1 (((1−t)^n )/(n!)) e^t dt .

$${provethat}\:{e}\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−{t}\right)^{{n}} }{{n}!}\:{e}^{{t}} \:{dt}\:. \\ $$

Question Number 34674 Answers: 0 Comments: 0

find ∫_0 ^π ((x sinx)/(1+cos^2 x)) dx

$${find}\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{x}\:{sinx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$

Question Number 34662 Answers: 0 Comments: 0

calculate I(a) =∫_(1/a) ^a ((ln(x))/(1+x^2 )) dx with a>0 2) calculate ∫_0 ^(+∞) ((ln(x))/(1+x^2 )) dx .

$${calculate}\:{I}\left({a}\right)\:\:=\int_{\frac{\mathrm{1}}{{a}}} ^{{a}} \:\:\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:. \\ $$

Question Number 34661 Answers: 0 Comments: 0

let f(x)= ∫_0 ^1 (e^(−(1+t^2 )x) /(1+t^2 )) dt find a simple form of f(x)

$${let}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{e}^{−\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:{find}\:{a}\:{simple}\:{form}\:{of} \\ $$$${f}\left({x}\right) \\ $$

Question Number 34635 Answers: 2 Comments: 4

calculate A(α) = ∫_0 ^1 ln(1+αix)dx 2) calculate ∫_0 ^1 ln(1+ix) dx (i^2 =−1)

$${calculate}\:{A}\left(\alpha\right)\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+\alpha{ix}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{ix}\right)\:{dx}\:\:\:\:\left({i}^{\mathrm{2}} \:=−\mathrm{1}\right) \\ $$

Question Number 34633 Answers: 0 Comments: 0

let f(α) = ∫_(−∞) ^(+∞) ((arctan(1+αxi))/(1+x^2 ))dx find f(α) .

$${let}\:{f}\left(\alpha\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{arctan}\left(\mathrm{1}+\alpha{xi}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${find}\:{f}\left(\alpha\right)\:. \\ $$

Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304

Terms of Service

Contact: info@tinkutara.com