
IntegrationQuestion and Answers: Page 297
Question Number 36167 Answers: 0 Comments: 2
Question Number 36057 Answers: 2 Comments: 1
Question Number 36056 Answers: 1 Comments: 2
Question Number 36031 Answers: 0 Comments: 0
Question Number 36009 Answers: 0 Comments: 1
Question Number 35990 Answers: 0 Comments: 2
Question Number 35983 Answers: 0 Comments: 1
Question Number 35982 Answers: 0 Comments: 0
Question Number 35949 Answers: 1 Comments: 1
Question Number 35920 Answers: 1 Comments: 1
$$\int\:\frac{{e}^{\mathrm{2}{x}} +\mathrm{1}}{\mathrm{2}{e}^{{x}} −\mathrm{1}}\:{dx}\:=\:? \\ $$
Question Number 35909 Answers: 1 Comments: 4
Question Number 35832 Answers: 1 Comments: 3
Question Number 35821 Answers: 0 Comments: 4
Question Number 35732 Answers: 1 Comments: 1
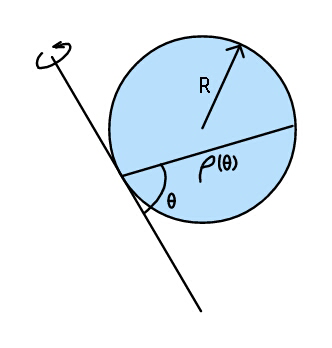
Question Number 35729 Answers: 1 Comments: 1
Question Number 35691 Answers: 0 Comments: 0
Question Number 35687 Answers: 1 Comments: 2
Question Number 35686 Answers: 1 Comments: 1
Question Number 35685 Answers: 1 Comments: 1
Question Number 35684 Answers: 1 Comments: 1
Question Number 35683 Answers: 1 Comments: 1
$${find}\:\int\:\:{x}^{\mathrm{2}} {ln}\left({x}^{\mathrm{6}} −\mathrm{1}\right){dx} \\ $$
Question Number 35682 Answers: 1 Comments: 2
Question Number 35681 Answers: 1 Comments: 1
Question Number 35680 Answers: 0 Comments: 0
Question Number 35678 Answers: 0 Comments: 1
Question Number 35677 Answers: 0 Comments: 2
Pg 292 Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301
