
IntegrationQuestion and Answers: Page 292
Question Number 37143 Answers: 0 Comments: 0
Question Number 37108 Answers: 1 Comments: 0
Question Number 37079 Answers: 1 Comments: 0
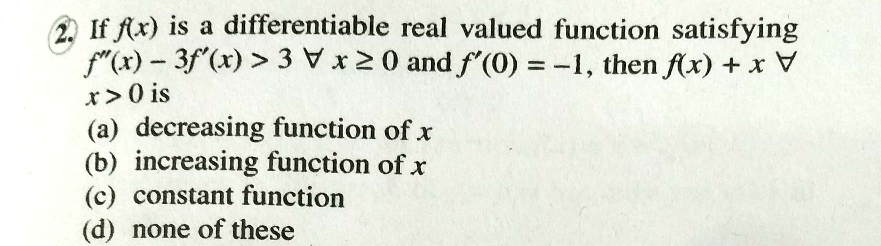
Question Number 37071 Answers: 2 Comments: 1
Question Number 37067 Answers: 2 Comments: 1
Question Number 37036 Answers: 0 Comments: 3
Question Number 37028 Answers: 1 Comments: 0
Question Number 37018 Answers: 3 Comments: 3

Question Number 37004 Answers: 3 Comments: 0

Question Number 36997 Answers: 2 Comments: 1
Question Number 36965 Answers: 2 Comments: 3
Question Number 36957 Answers: 2 Comments: 0
Question Number 36946 Answers: 0 Comments: 2
Question Number 36945 Answers: 0 Comments: 0
Question Number 36944 Answers: 1 Comments: 1
Question Number 36943 Answers: 0 Comments: 1
Question Number 36942 Answers: 1 Comments: 0
Question Number 36941 Answers: 0 Comments: 1
Question Number 36940 Answers: 0 Comments: 1
Question Number 36939 Answers: 0 Comments: 0
Question Number 36938 Answers: 0 Comments: 2
Question Number 36937 Answers: 0 Comments: 1
$${calculate}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{x}\:{dx}}{\mathrm{1}+{cosx}} \\ $$
Question Number 36936 Answers: 0 Comments: 2
Question Number 36935 Answers: 0 Comments: 0
Question Number 36932 Answers: 0 Comments: 0
Question Number 36931 Answers: 0 Comments: 2
$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{x}\:−{e}^{{it}} } \\ $$
Pg 287 Pg 288 Pg 289 Pg 290 Pg 291 Pg 292 Pg 293 Pg 294 Pg 295 Pg 296
