
IntegrationQuestion and Answers: Page 280
Question Number 40868 Answers: 0 Comments: 4
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{{sinx}}{dx}\:\:. \\ $$
Question Number 40830 Answers: 0 Comments: 1
$${find}\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {t}}{dt} \\ $$
Question Number 40829 Answers: 1 Comments: 0
Question Number 40823 Answers: 0 Comments: 1
Question Number 40787 Answers: 1 Comments: 4
Question Number 40760 Answers: 0 Comments: 0
Question Number 40745 Answers: 3 Comments: 0
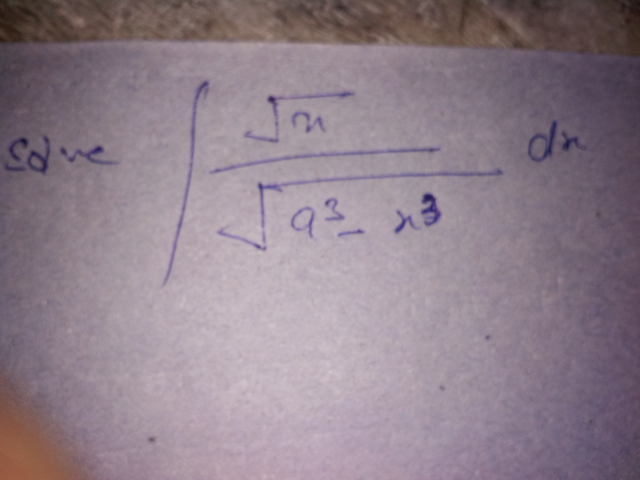
Question Number 40717 Answers: 1 Comments: 1
Question Number 40716 Answers: 2 Comments: 0
$$\int\left({cosx}−{cos}\mathrm{2}{x}/\mathrm{1}−{cosx}\right){dx} \\ $$
Question Number 40684 Answers: 0 Comments: 1
$$\int\frac{\mathrm{x}^{\mathrm{7}} −\mathrm{1}}{\mathrm{logx}}\mathrm{dx} \\ $$
Question Number 40675 Answers: 1 Comments: 2

Question Number 40661 Answers: 0 Comments: 4
Question Number 40660 Answers: 0 Comments: 0
Question Number 40658 Answers: 0 Comments: 1
Question Number 40657 Answers: 1 Comments: 0

Question Number 41351 Answers: 1 Comments: 3
Question Number 40625 Answers: 2 Comments: 0

Question Number 40624 Answers: 0 Comments: 0
Question Number 40621 Answers: 2 Comments: 0
Question Number 40620 Answers: 3 Comments: 0
Question Number 40619 Answers: 0 Comments: 2
Question Number 40580 Answers: 0 Comments: 3
Question Number 40569 Answers: 0 Comments: 0

Question Number 40505 Answers: 1 Comments: 0
Question Number 40442 Answers: 2 Comments: 0
Question Number 40422 Answers: 1 Comments: 1
$$\mathrm{Solve}: \\ $$$$\mathrm{yd}{x}\:−\:{xdy}\:+\mathrm{log}\:{xdx}\:=\mathrm{0} \\ $$
Pg 275 Pg 276 Pg 277 Pg 278 Pg 279 Pg 280 Pg 281 Pg 282 Pg 283 Pg 284
