Question and Answers Forum

IntegrationQuestion and Answers: Page 28

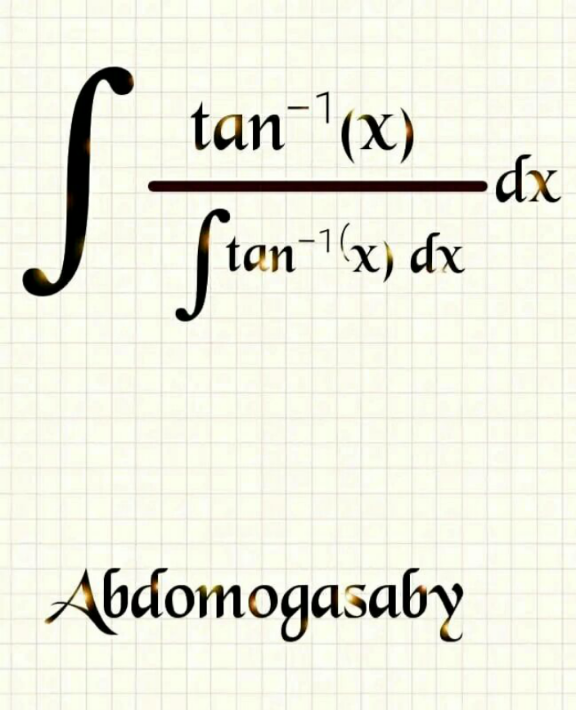
Question Number 200061 Answers: 1 Comments: 0

∫_(−∞) ^(+∞) ((xsinx )/((x^2 +1)(x^2 +4)))dx = ??

$$\:\:\:\:\int_{−\infty} ^{+\infty} \frac{{x}\mathrm{sin}{x}\:}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}\:\:=\:\:\:?? \\ $$

Question Number 199942 Answers: 1 Comments: 0

Question Number 199934 Answers: 2 Comments: 0

y=f(x), x≥0 f(3x)= 3f(x). If ∫_3 ^(27) f(x)dx= 10 than ∫_0 ^3 f(x) dx =?

$$\:\: \mathrm{y}=\mathrm{f}\left(\mathrm{x}\right),\:\mathrm{x}\geqslant\mathrm{0}\: \\ $$$$\: \mathrm{f}\left(\mathrm{3x}\right)=\:\mathrm{3f}\left(\mathrm{x}\right).\:\mathrm{If}\:\underset{\mathrm{3}} {\overset{\mathrm{27}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\:\mathrm{10} \\ $$$$\:\mathrm{than}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=?\: \\ $$

Question Number 199921 Answers: 1 Comments: 0

Question Number 199907 Answers: 1 Comments: 0

∫ (dx/( (√x) + (x)^(1/3) )) =?

$$\:\:\:\:\:\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{x}}}\:=?\: \\ $$

Question Number 199903 Answers: 2 Comments: 1

∫((x^2 dx)/( (√(x^2 −16)))) = ?

$$\int\frac{{x}^{\mathrm{2}} {dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}}\:=\:? \\ $$

Question Number 199598 Answers: 0 Comments: 0

Question Number 199570 Answers: 1 Comments: 0

I = ∫_0 ^(π/2) tan^(−1) (((sinx )/2))dx

$$\:\:\:\:\:\:\:\:\mathrm{I}\:\:\:\:\:=\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}{x}\:}{\mathrm{2}}\right){dx} \\ $$

Question Number 199471 Answers: 1 Comments: 0

Find the integral ∫_(−3) ^3 { ((x^3 −x),((x≤0))),(x^2 ,((x≥0))) :}dx

$${Find}\:{the}\:{integral} \\ $$$$\int_{−\mathrm{3}} ^{\mathrm{3}} \begin{cases}{{x}^{\mathrm{3}} −{x}}&{\left({x}\leq\mathrm{0}\right)}\\{{x}^{\mathrm{2}} }&{\left({x}\geq\mathrm{0}\right)}\end{cases}{dx} \\ $$

Question Number 199468 Answers: 1 Comments: 0

Question Number 199377 Answers: 1 Comments: 0

∫∫_R cos (max{x^3 , y^(3/2) })dx dy , where R = [0,1]×[0,1]

$$\:\:\int\underset{\mathrm{R}} {\int}\mathrm{cos}\:\left(\mathrm{max}\left\{\mathrm{x}^{\mathrm{3}} ,\:\mathrm{y}^{\mathrm{3}/\mathrm{2}} \right\}\right)\mathrm{dx}\:\mathrm{dy}\:,\:\mathrm{where}\:\mathrm{R}\:=\:\left[\mathrm{0},\mathrm{1}\right]×\left[\mathrm{0},\mathrm{1}\right] \\ $$

Question Number 199369 Answers: 0 Comments: 0

∫_(−1) ^1 ∫_(−(√(1−x^2 ))) ^(√(1−x^2 )) ∫_(1−(√(1−x^2 −y^2 ))) ^(1+(√(1−y^2 ))) (x^2 +y^2 +z^2 )^(5/2) dx dy dz is

$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:\int_{−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} \:}} ^{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \:\int_{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }} ^{\mathrm{1}+\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} {dx}\:{dy}\:{dz}\:\:{is} \\ $$

Question Number 199213 Answers: 1 Comments: 0

Question Number 199162 Answers: 0 Comments: 0

x=−2(√3)∫y^3 (√(1+(1/y))) dy Find ∫x(y)dy .

$${x}=−\mathrm{2}\sqrt{\mathrm{3}}\int{y}^{\mathrm{3}} \sqrt{\mathrm{1}+\frac{\mathrm{1}}{{y}}}\:{dy} \\ $$$${Find}\:\:\int{x}\left({y}\right){dy}\:\:\:. \\ $$

Question Number 198948 Answers: 2 Comments: 0

∫_1 ^3 ((x−2)/(x^2 −4x)) dx= ....

$$\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}}\:\mathrm{dx}=\:.... \\ $$

Question Number 198929 Answers: 0 Comments: 0

Question Number 198802 Answers: 1 Comments: 0

radius r circle ; x^2 +y^2 +z^2 =r^2 F^ (x,y,z)=yze_1 ^ +xe_2 ^ −xye_3 ^ Find flux 𝛒=∫∫_( 𝚺) F^ ∙n^ dS

$$\mathrm{radius}\:{r}\:\mathrm{circle}\:;\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\hat {\boldsymbol{\mathrm{F}}}\left({x},{y},{z}\right)={yz}\hat {\boldsymbol{\mathrm{e}}}_{\mathrm{1}} +{x}\hat {\boldsymbol{\mathrm{e}}}_{\mathrm{2}} −{xy}\hat {\boldsymbol{\mathrm{e}}}_{\mathrm{3}} \\ $$$$\mathrm{Find}\:\mathrm{flux}\:\boldsymbol{\rho}=\int\int_{\:\boldsymbol{\Sigma}} \:\hat {\boldsymbol{\mathrm{F}}}\centerdot\hat {\boldsymbol{\mathrm{n}}}\:\mathrm{d}{S} \\ $$

Question Number 198731 Answers: 2 Comments: 2

Question Number 198695 Answers: 1 Comments: 0

∫_0 ^∞ ((e^(at) −e^(−at) )/(e^(πt) −e^(−πt) )) dt = ??

$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{\mathrm{at}} −\mathrm{e}^{−\mathrm{at}} }{\mathrm{e}^{\pi\mathrm{t}} −\mathrm{e}^{−\pi\mathrm{t}} }\:\mathrm{dt}\:\:\:=\:\:\:?? \\ $$

Question Number 198497 Answers: 0 Comments: 0

∫_0 ^∞ ((e^(at) −e^(−at) )/(e^(πt) −e^(−πt) )) dt

$$\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{\mathrm{at}} −\mathrm{e}^{−\mathrm{at}} }{\mathrm{e}^{\pi\mathrm{t}} −\mathrm{e}^{−\pi\mathrm{t}} }\:\mathrm{dt} \\ $$

Question Number 198496 Answers: 1 Comments: 0

A nice series If , Ω = Σ_(n=2) ^∞ (( 1)/(n^( 2) +n −1)) =(( π tan( aπ ))/( b)) ⇒ find the value of (b/a) = ?

$$ \\ $$$$\:\:\:\:\:\:\:\:\:{A}\:{nice}\:\:{series} \\ $$$$\:\:{If}\:,\:\:\Omega\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\:\mathrm{1}}{{n}^{\:\mathrm{2}} \:+{n}\:−\mathrm{1}}\:=\frac{\:\pi\:{tan}\left(\:{a}\pi\:\right)}{\:{b}} \\ $$$$\:\:\:\:\:\Rightarrow\:{find}\:{the}\:{value}\:{of}\:\:\:\frac{{b}}{{a}}\:=\:? \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$

Question Number 198420 Answers: 1 Comments: 0

Question Number 198419 Answers: 0 Comments: 0

Please Help... ∫∫_S x^2 dydz+y^2 dzdx+2z(xy−x−y)dxdy where S is the surface of the cube. 0≤x≤1, 0≤y≤1, 0≤z≤1

$$\:\:{Please}\:{Help}... \\ $$$$\:\:\int\underset{{S}} {\int}{x}^{\mathrm{2}} {dydz}+{y}^{\mathrm{2}} {dzdx}+\mathrm{2}{z}\left({xy}−{x}−{y}\right){dxdy}\:{where} \\ $$$$\:\:\:{S}\:{is}\:{the}\:{surface}\:{of}\:{the}\:{cube}.\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1},\:\mathrm{0}\leqslant{y}\leqslant\mathrm{1}, \\ $$$$\:\:\:\:\mathrm{0}\leqslant{z}\leqslant\mathrm{1} \\ $$$$ \\ $$

Question Number 198403 Answers: 1 Comments: 0

Question Number 198001 Answers: 0 Comments: 2

∫(e)^((x)^(lnx) ) dx=?

$$\int\left({e}\right)^{\left({x}\right)^{{lnx}} } \:{dx}=? \\ $$

Question Number 197919 Answers: 1 Comments: 0

I_m = ∫_0 ^1 (((⌊2^m x⌋)/3^m ) Σ_(n=m+1) ^∞ ((⌊2^n x⌋)/3^n ))dx then find the value of I = Σ_(m=1) ^∞ I_m = ?

$$\:\:\:\:\:\:\mathrm{I}_{{m}} \:\:\:\:\:=\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\lfloor\mathrm{2}^{{m}} {x}\rfloor}{\mathrm{3}^{{m}} }\:\underset{{n}={m}+\mathrm{1}} {\overset{\infty} {\sum}}\frac{\lfloor\mathrm{2}^{{n}} {x}\rfloor}{\mathrm{3}^{{n}} }\right){dx} \\ $$$$\:\:\:\:\:\:\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\:\:\:\:\:\:\mathrm{I}\:=\:\:\:\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{I}_{{m}} \:\:=\:\:?\: \\ $$

Pg 23 Pg 24 Pg 25 Pg 26 Pg 27 Pg 28 Pg 29 Pg 30 Pg 31 Pg 32

Contact: info@tinkutara.com