Question and Answers Forum

IntegrationQuestion and Answers: Page 277

Question Number 42305 Answers: 0 Comments: 6

let f(x) = ∫_(−∞) ^(+∞) ((cos(xt))/((t−i)^2 )) dt 1) let R =Re(f(x)) and I =Im(f(x)) extract R and I 2) calculate R and I 3) conclude the value of f(x) 4) calculate ∫_(−∞) ^(+∞) ((cos(2t))/((t−i)^2 ))dt 5) let u_n = ∫_(−∞) ^(+∞) ((cos((t/n)))/((t−i)^2 ))dt (n natral integer not o) find lim_(n→+∞) u_n and study the convergence of Σu_n

$${let}\:{f}\left({x}\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left({xt}\right)}{\left({t}−{i}\right)^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{let}\:{R}\:={Re}\left({f}\left({x}\right)\right)\:{and}\:{I}\:={Im}\left({f}\left({x}\right)\right)\:{extract}\:{R}\:{and}\:{I} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{R}\:{and}\:{I} \\ $$$$\left.\mathrm{3}\right)\:{conclude}\:{the}\:{value}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{\left({t}−{i}\right)^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{5}\right)\:{let}\:{u}_{{n}} =\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\frac{{t}}{{n}}\right)}{\left({t}−{i}\right)^{\mathrm{2}} }{dt}\:\:\:\:\left({n}\:{natral}\:{integer}\:{not}\:{o}\right) \\ $$$${find}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} \:\:\:\:{and}\:\:{study}\:{the}\:{convergence}\:{of}\:\Sigma{u}_{{n}} \\ $$

Question Number 42228 Answers: 1 Comments: 0

Solve : 2x^2 ydx −2y^4 dx+2x^3 dy+3xy^3 dy=0.

$$\mathrm{Solve}\:: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} {ydx}\:−\mathrm{2}{y}^{\mathrm{4}} {dx}+\mathrm{2}{x}^{\mathrm{3}} {dy}+\mathrm{3}{xy}^{\mathrm{3}} {dy}=\mathrm{0}. \\ $$

Question Number 42222 Answers: 1 Comments: 0

let f(x) =e^(−∣x∣) , 2π periodic even developp f at fourier serie .

$${let}\:{f}\left({x}\right)\:={e}^{−\mid{x}\mid} \:,\:\:\mathrm{2}\pi\:{periodic}\:{even}\:\:{developp}\:{f}\:{at}\:{fourier}\:{serie}\:. \\ $$

Question Number 42221 Answers: 1 Comments: 0

Solve: (dt/dx) = (2/(x+t)) .

$$\mathrm{Solve}: \\ $$$$\frac{\mathrm{dt}}{\mathrm{d}{x}}\:=\:\frac{\mathrm{2}}{{x}+\mathrm{t}}\:. \\ $$

Question Number 42215 Answers: 0 Comments: 3

Number of straight lines which satisfy the differential equation (dy/dx) + x((dy/dx))^2 − y =0 is ?

$$\mathrm{Number}\:\mathrm{of}\:\mathrm{straight}\:\mathrm{lines}\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\frac{\mathrm{dy}}{{dx}}\:+\:{x}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} −\:{y}\:=\mathrm{0}\:{is}\:? \\ $$

Question Number 42191 Answers: 0 Comments: 1

let A_p =∫_0 ^∞ ((sin(px))/(e^x −1)) dx with p>0 1)give A_p at form of serie 2) give A_1 at form of serie .

$${let}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({px}\right)}{{e}^{{x}} −\mathrm{1}}\:{dx}\:\:{with}\:{p}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right){give}\:{A}_{{p}} \:\:{at}\:{form}\:{of}\:{serie} \\ $$$$\left.\mathrm{2}\right)\:{give}\:{A}_{\mathrm{1}} \:{at}\:{form}\:{of}\:{serie}\:. \\ $$

Question Number 42189 Answers: 0 Comments: 0

calculate f(x) = ∫_0 ^∞ e^(−t^2 ) arctan(xt^2 )dt

$${calculate}\:\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \:{arctan}\left({xt}^{\mathrm{2}} \right){dt} \\ $$

Question Number 42188 Answers: 0 Comments: 1

let x>0 calculate f(x) =∫_0 ^(+∞) e^(−t) ∣sin(xt)∣ dt

$${let}\:{x}>\mathrm{0}\:\:\:{calculate}\:\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{+\infty} \:\:{e}^{−{t}} \:\mid{sin}\left({xt}\right)\mid\:{dt} \\ $$

Question Number 42232 Answers: 1 Comments: 0

calculate ∫_0 ^(2π) (dθ/((1+cosθ)^3 ))

$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{d}\theta}{\left(\mathrm{1}+{cos}\theta\right)^{\mathrm{3}} } \\ $$

Question Number 42157 Answers: 0 Comments: 3

∫_( 0) ^( ∞) (dx/((1 + x^n )))

$$\:\int_{\:\mathrm{0}} ^{\:\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}\:+\:\mathrm{x}^{\mathrm{n}} \right)} \\ $$

Question Number 42088 Answers: 1 Comments: 1

find ∫ (1+(1/x^2 ))ln(1−(1/x))dx .

$${find}\:\:\:\:\:\int\:\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx}\:\:. \\ $$

Question Number 42087 Answers: 0 Comments: 0

find ∫ ((x dx)/(x(√(1+x^2 )) +(1+x^2 )(√x)))

$${find}\:\:\:\:\int\:\:\:\:\:\:\:\:\frac{{x}\:{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}}} \\ $$

Question Number 42086 Answers: 1 Comments: 0

let f(x) =∫_0 ^2 ((ch(t))/(2xsh(t) +1)) dt 1) find a simple form of f(x) 2) calculate ∫_0 ^2 ((ch(t))/(1+sh(t)))dt 3) calculate ∫_0 ^2 ((ch(t))/(3sh(t) +1))dt .

$${let}\:\:\:\:{f}\left({x}\right)\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\:\frac{{ch}\left({t}\right)}{\mathrm{2}{xsh}\left({t}\right)\:+\mathrm{1}}\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:\:{a}\:{simple}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\frac{{ch}\left({t}\right)}{\mathrm{1}+{sh}\left({t}\right)}{dt} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\frac{{ch}\left({t}\right)}{\mathrm{3}{sh}\left({t}\right)\:+\mathrm{1}}{dt}\:. \\ $$

Question Number 42085 Answers: 1 Comments: 1

calculate ∫_1 ^(+∞) ((2x+1)/(3 +(x+1)^3 ))dx

$${calculate}\:\:\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}\:+\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{dx}\: \\ $$

Question Number 42083 Answers: 0 Comments: 0

calculate ∫_0 ^1 ((2x+1)/(3+(1+x)^3 ))dx

$${calculate}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}+\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }{dx} \\ $$

Question Number 42054 Answers: 1 Comments: 1

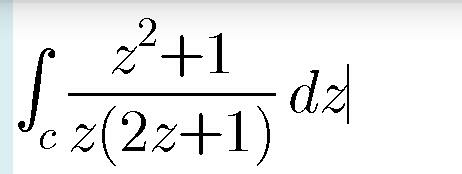
Question Number 42012 Answers: 2 Comments: 0

Solve : (du/dt) = ((3u−7t)/(−7u+3t))

$$\mathrm{Solve}\:: \\ $$$$\frac{{d}\mathrm{u}}{{d}\mathrm{t}}\:=\:\frac{\mathrm{3u}−\mathrm{7t}}{−\mathrm{7u}+\mathrm{3t}} \\ $$

Question Number 41989 Answers: 2 Comments: 1

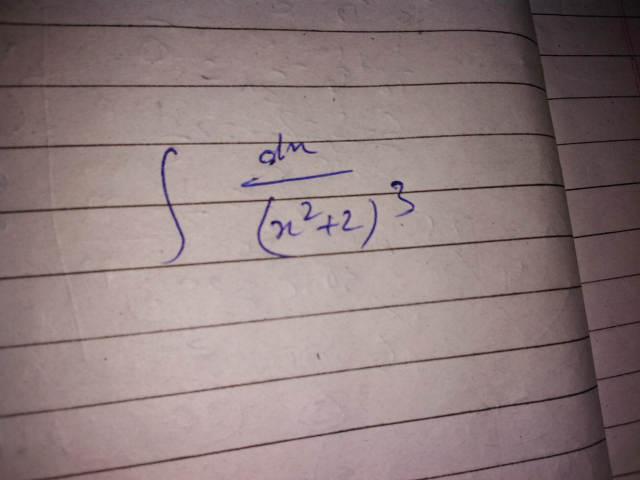
Question Number 41913 Answers: 1 Comments: 0

let f(a) = ∫_0 ^π (x/(1+acosx))dx 1) find f(a) 2) calculate ∫_0 ^π (x/(1+2cosx))dx and ∫_0 ^π (x/(1−2cosx))dx 3) calculate ∫_0 ^π ((xcosx)/((1+acosx)^2 ))dx 4) find the value of ∫_0 ^π ((xcosx)/((1+2cosx)^2 ))dx .

$${let}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{x}}{\mathrm{1}+{acosx}}{dx} \\ $$$$\left.\mathrm{1}\right)\:{find}\:\:{f}\left({a}\right)\: \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{x}}{\mathrm{1}+\mathrm{2}{cosx}}{dx}\:{and}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{x}}{\mathrm{1}−\mathrm{2}{cosx}}{dx} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{xcosx}}{\left(\mathrm{1}+{acosx}\right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{4}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{xcosx}}{\left(\mathrm{1}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }{dx}\:. \\ $$

Question Number 41854 Answers: 0 Comments: 0

1)calculate ∫_0 ^1 ln(1+x+x^2 +x^3 )dx 2)then find the value of ∫_0 ^1 ln( 1−x^5 ) dx 3) find the value of Σ_(n=1) ^∞ (1/(n(5n+1))) .

$$\left.\mathrm{1}\right){calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{3}} \right){dx} \\ $$$$\left.\mathrm{2}\right){then}\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\:\mathrm{1}−{x}^{\mathrm{5}} \right)\:{dx} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}\left(\mathrm{5}{n}+\mathrm{1}\right)}\:. \\ $$$$ \\ $$$$ \\ $$

Question Number 41851 Answers: 0 Comments: 2

Question Number 41847 Answers: 1 Comments: 0

let f(x) = ∫_0 ^(π/4) (dt/(x +tan(t))) 1) find anoher expression off (x) 2) calculate ∫_0 ^(π/4) (dt/(2+tan(t))) and A(θ) = ∫_0 ^(π/4) (dt/(sinθ+tant)) 3) calculate ∫_0 ^(π/4) (dt/((1+tant)^2 ))

$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{dt}}{{x}\:+{tan}\left({t}\right)} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{anoher}\:{expression}\:{off}\:\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\mathrm{2}+{tan}\left({t}\right)}\:\:\:{and}\:\:{A}\left(\theta\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{{sin}\theta+{tant}} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{tant}\right)^{\mathrm{2}} } \\ $$

Question Number 41846 Answers: 1 Comments: 0

find ∫ (dx/((√(1+x^2 )) +(√(1−x^2 ))))

$${find}\:\:\int\:\:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:\:+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$

Question Number 41845 Answers: 1 Comments: 0

1)find ∫ (x/((√(1+x)) +(√(1−x)))) dx 2) calculate ∫_1 ^3 (x/((√(1+x)) +(√(1−x)))) dx

$$\left.\mathrm{1}\right){find}\:\:\:\:\int\:\:\:\:\:\:\:\:\:\frac{{x}}{\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}−{x}}}\:{dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\:\:\frac{{x}}{\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}−{x}}}\:{dx} \\ $$

Question Number 41848 Answers: 0 Comments: 3

let f(a) = ∫_0 ^(π/2) (dx/(1+asinx)) with a∈R 1) find a simple form of f(a) 2) calculate ∫_0 ^(π/2) (dx/(1+sinx)) and ∫_0 ^(π/2) (dx/(1+2sinx)) 3) find the value of ∫_0 ^(π/2) ((cosx)/((1+asinx)^2 ))dx 4) find the value of ∫_0 ^(π/2) ((cosx)/((1+sinx)^2 ))dx and ∫_0 ^(π/2) ((cosx)/((1+2sinx)^2 ))dx

$${let}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dx}}{\mathrm{1}+{asinx}}\:\:\:{with}\:{a}\in{R} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{1}+{sinx}}\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\mathrm{1}+\mathrm{2}{sinx}} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cosx}}{\left(\mathrm{1}+{asinx}\right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{4}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cosx}}{\left(\mathrm{1}+{sinx}\right)^{\mathrm{2}} }{dx}\:{and}\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cosx}}{\left(\mathrm{1}+\mathrm{2}{sinx}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 41806 Answers: 1 Comments: 1

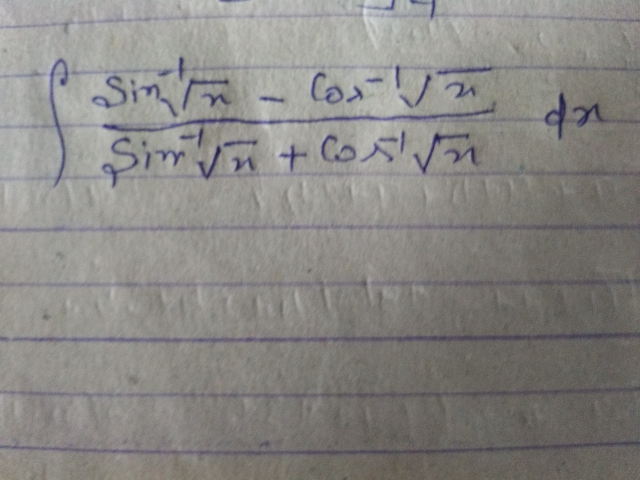
Pg 272 Pg 273 Pg 274 Pg 275 Pg 276 Pg 277 Pg 278 Pg 279 Pg 280 Pg 281

Contact: info@tinkutara.com