
IntegrationQuestion and Answers: Page 269
Question Number 45019 Answers: 1 Comments: 0
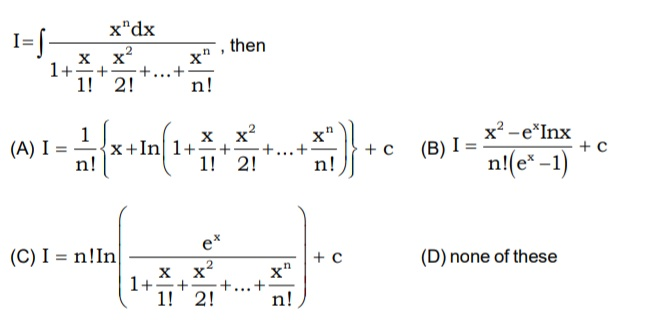
Question Number 44994 Answers: 1 Comments: 0
Question Number 44993 Answers: 1 Comments: 1
$$\int\frac{\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx}=? \\ $$
Question Number 44992 Answers: 2 Comments: 0
Question Number 44921 Answers: 1 Comments: 1
$$\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{ln}\:\mathrm{x}}=? \\ $$
Question Number 44781 Answers: 2 Comments: 0
Question Number 44778 Answers: 0 Comments: 0
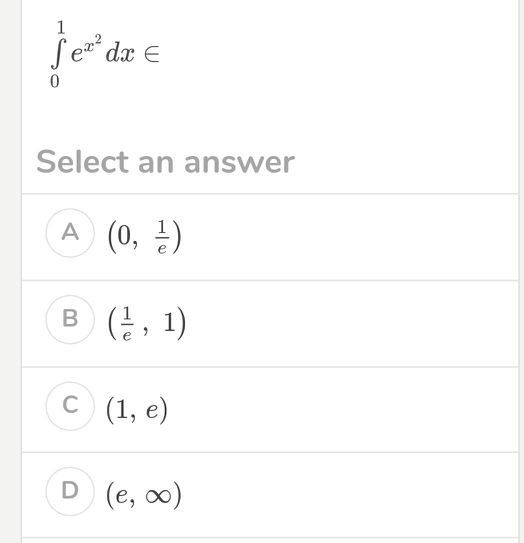
Question Number 44777 Answers: 0 Comments: 0
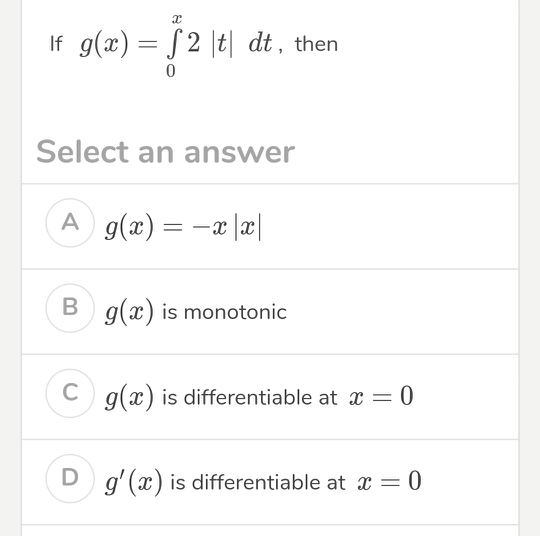
Question Number 44712 Answers: 3 Comments: 0

Question Number 44702 Answers: 0 Comments: 0

Question Number 44697 Answers: 0 Comments: 0
Question Number 44706 Answers: 0 Comments: 4
Question Number 44696 Answers: 1 Comments: 1
Question Number 44695 Answers: 0 Comments: 2
Question Number 44639 Answers: 0 Comments: 1
Question Number 44654 Answers: 1 Comments: 4
Question Number 44604 Answers: 1 Comments: 1
Question Number 44602 Answers: 0 Comments: 0
Question Number 44587 Answers: 1 Comments: 2
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2018}} } \\ $$
Question Number 44674 Answers: 0 Comments: 1
Question Number 44573 Answers: 1 Comments: 1

Question Number 44575 Answers: 1 Comments: 3

Question Number 44515 Answers: 1 Comments: 0
Question Number 44512 Answers: 1 Comments: 1
Question Number 44509 Answers: 1 Comments: 1
$$\int\sqrt{\boldsymbol{\mathrm{tan}}\:\boldsymbol{\mathrm{x}}}\:\:\boldsymbol{\mathrm{dx}}=? \\ $$
Question Number 44508 Answers: 1 Comments: 1
$$\int\sqrt{\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\:}\boldsymbol{\mathrm{dx}}=? \\ $$
Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272 Pg 273
