
IntegrationQuestion and Answers: Page 268
Question Number 45519 Answers: 0 Comments: 2
$${find}\:\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}{d}\theta \\ $$
Question Number 45498 Answers: 1 Comments: 3

Question Number 45495 Answers: 1 Comments: 0
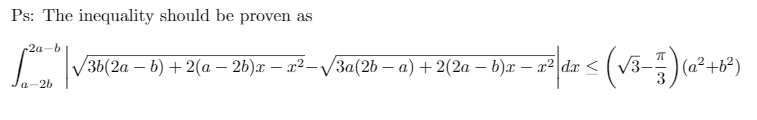
Question Number 45482 Answers: 1 Comments: 0
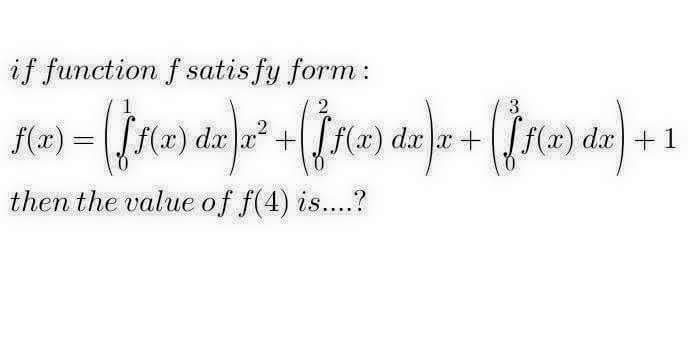
Question Number 45373 Answers: 1 Comments: 1
$$\int\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}=? \\ $$
Question Number 45352 Answers: 1 Comments: 0

Question Number 45334 Answers: 1 Comments: 0
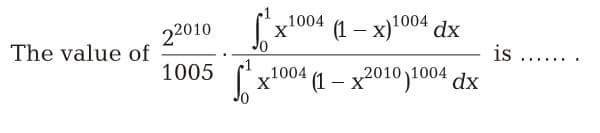
Question Number 45264 Answers: 0 Comments: 4

Question Number 45235 Answers: 0 Comments: 2
Question Number 45201 Answers: 0 Comments: 6
$${find}\:\int\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }} \\ $$
Question Number 45232 Answers: 1 Comments: 1
Question Number 45231 Answers: 2 Comments: 1
$${find}\:\int\:\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{3}−{x}\right)}{dx} \\ $$
Question Number 45155 Answers: 2 Comments: 1

Question Number 45151 Answers: 0 Comments: 2
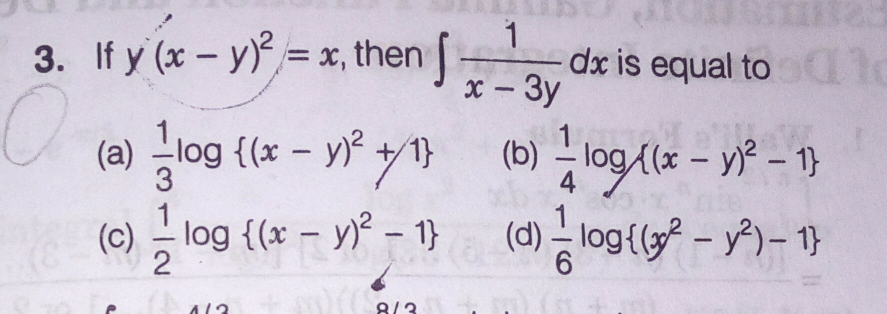
Question Number 45165 Answers: 1 Comments: 0

Question Number 45164 Answers: 0 Comments: 6

Question Number 45158 Answers: 0 Comments: 1
Question Number 45128 Answers: 1 Comments: 1

Question Number 45117 Answers: 1 Comments: 3
Question Number 45075 Answers: 1 Comments: 2
Question Number 45063 Answers: 0 Comments: 2
Question Number 45045 Answers: 1 Comments: 0
Question Number 45044 Answers: 0 Comments: 1
Question Number 45043 Answers: 3 Comments: 0
Question Number 45021 Answers: 2 Comments: 0
Question Number 45020 Answers: 2 Comments: 5

Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272
