Question and Answers Forum

some practice for the brave... ∫((cos^2 x sin^2 x)/(cos x +sin x))dx=? ∫((cos^2 x tan^2 x)/(cos x +tan x))dx=? ∫((sin^2 x tan^2 x)/(sin x +tan x))dx=?

$$\mathrm{some}\:\mathrm{practice}\:\mathrm{for}\:\mathrm{the}\:\mathrm{brave}... \\ $$$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{dx}=? \\ $$$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{cos}\:{x}\:+\mathrm{tan}\:{x}}{dx}=? \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{sin}\:{x}\:+\mathrm{tan}\:{x}}{dx}=? \\ $$

Question Number 45795 Answers: 1 Comments: 0

find ∫ (dx/(cosx sin^2 x))

$${find}\:\int\:\frac{{dx}}{{cosx}\:{sin}^{\mathrm{2}} {x}} \\ $$

Question Number 45771 Answers: 1 Comments: 0

find f(x)=∫_0 ^∞ cos(x+t^2 )dtand g(x)=∫_0 ^∞ sin(x+t^2 )dt 2) find the value of f^′ (x) and g^′ (x).

$${find}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}+{t}^{\mathrm{2}} \right){dtand}\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{sin}\left({x}+{t}^{\mathrm{2}} \right){dt} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:{f}^{'} \left({x}\right)\:{and}\:{g}^{'} \left({x}\right). \\ $$

Question Number 45735 Answers: 2 Comments: 1

∫_α ^β (1/((x−α)(β−x)))dx =? β>α

$$\int_{\alpha} ^{\beta} \frac{\mathrm{1}}{\left({x}−\alpha\right)\left(\beta−{x}\right)}{dx}\:\:=?\:\:\:\beta>\alpha \\ $$

Question Number 45721 Answers: 0 Comments: 3

Integrate sin (x^2 )dx

$$\:{Integrate}\:\mathrm{sin}\:\left({x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 45706 Answers: 1 Comments: 0

Question Number 45705 Answers: 0 Comments: 3

Question Number 45670 Answers: 1 Comments: 1

∫cos^(−1) (sinx)dx=?

$$\int{cos}^{−\mathrm{1}} \left({sinx}\right){dx}=? \\ $$

Question Number 45669 Answers: 2 Comments: 0

∫tan^(−1) (√((1−sinx)/(1+sinx))) dx=?

$$\int{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{sinx}}{\mathrm{1}+{sinx}}}\:{dx}=? \\ $$

Question Number 45641 Answers: 2 Comments: 1

Question Number 45634 Answers: 0 Comments: 0

1)find ∫ ln(1−x^6 )dx 2) calculate ∫_0 ^1 ln(1−x^6 )dx

$$\left.\mathrm{1}\right){find}\:\int\:{ln}\left(\mathrm{1}−{x}^{\mathrm{6}} \right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{6}} \right){dx} \\ $$

Question Number 45632 Answers: 0 Comments: 2

1)find ∫ ln(1+x^3 )dx 2) calculate ∫_0 ^1 ln(1+x^3 )ex

$$\left.\mathrm{1}\right){find}\:\int\:{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){ex} \\ $$

Question Number 45600 Answers: 0 Comments: 2

find f(x,y) =∫_0 ^(π/2) ln(x+y sinθ)dθ with ∣y∣<∣x∣ 2) find f(2,3) 3)find f((√2),(√3)) .

$${find}\:{f}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({x}+{y}\:{sin}\theta\right){d}\theta\:\:{with}\:\:\mid{y}\mid<\mid{x}\mid \\ $$$$\left.\mathrm{2}\right)\:{find}\:{f}\left(\mathrm{2},\mathrm{3}\right) \\ $$$$\left.\mathrm{3}\right){find}\:{f}\left(\sqrt{\mathrm{2}},\sqrt{\mathrm{3}}\right)\:. \\ $$

Question Number 45561 Answers: 0 Comments: 2

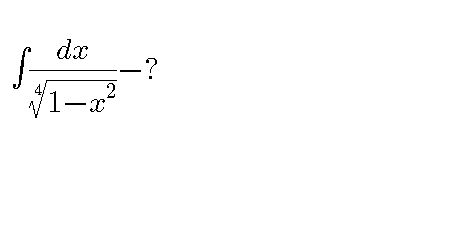
Question Number 45520 Answers: 0 Comments: 1

let a>0 and b>0 calculate ∫ (√(acos^2 θ +bsin^2 θ))dπ 2) find ∫_(π/4) ^(π/2) (√(2cos^2 θ +3 sin^2 θ))dθ .

$${let}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0}\:{calculate}\:\int\:\sqrt{{acos}^{\mathrm{2}} \theta\:+{bsin}^{\mathrm{2}} \theta}{d}\pi \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{2}{cos}^{\mathrm{2}} \theta\:+\mathrm{3}\:{sin}^{\mathrm{2}} \theta}{d}\theta\:. \\ $$

Question Number 45519 Answers: 0 Comments: 2

find ∫ (√(2+tan^2 θ))dθ

$${find}\:\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}{d}\theta \\ $$

Question Number 45498 Answers: 1 Comments: 3

Pg 262 Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271

Contact: info@tinkutara.com