Question and Answers Forum

IntegrationQuestion and Answers: Page 263

Question Number 48104 Answers: 1 Comments: 0

solve this ∫(2 sinx+cosx)/(2+3sinx+sin^(2x) ) dx

$$\mathrm{solve}\:\mathrm{this}\:\: \\ $$$$\int\left(\mathrm{2}\:\mathrm{sinx}+\mathrm{cosx}\right)/\left(\mathrm{2}+\mathrm{3sinx}+\mathrm{sin}^{\mathrm{2x}} \right)\:\mathrm{dx} \\ $$

Question Number 48078 Answers: 1 Comments: 0

Question Number 48067 Answers: 0 Comments: 1

let y>0 give ∫_0 ^∞ (x^y /(e^x −1))dx at form of series.

$${let}\:{y}>\mathrm{0}\:{give}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{y}} }{{e}^{{x}} −\mathrm{1}}{dx}\:{at}\:{form}\:{of}\:{series}. \\ $$

Question Number 48064 Answers: 1 Comments: 1

calculate A =∫_0 ^1 (1+x^2 )(√(1−x^2 ))dx −∫_0 ^1 (1−x^2 )(√(1+x^2 ))dx

$${calculate}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 48063 Answers: 0 Comments: 0

let W(x) =∫_(−∞) ^(+∞) ((arctan(xt^2 ))/(2+t^2 ))dt 1) find a explicit form of f(x) 2) find the value of ∫_(−∞) ^(+∞) (t^2 /((2+t^2 )(1+x^2 t^4 )))dt .

$${let}\:{W}\left({x}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{arctan}\left({xt}^{\mathrm{2}} \right)}{\mathrm{2}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{2}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} \right)}{dt}\:. \\ $$

Question Number 48062 Answers: 0 Comments: 0

calculate ∫_(−∞) ^(+∞) (((x^2 −3)sin(2x^2 ))/((x^2 +1)^3 ))dx

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{\left({x}^{\mathrm{2}} −\mathrm{3}\right){sin}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$

Question Number 48057 Answers: 2 Comments: 1

Question Number 48043 Answers: 0 Comments: 1

let f(α) =∫_(−∞) ^(+∞) ((cos(αx^3 ))/(x^2 +8)) dx 1)calculate f(α) 2) calculate ∫_(−∞) ^(+∞) ((cos(2x^3 ))/(x^2 +8))dx .

$${let}\:{f}\left(\alpha\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left(\alpha{x}^{\mathrm{3}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{8}}\:{dx} \\ $$$$\left.\mathrm{1}\right){calculate}\:{f}\left(\alpha\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left(\mathrm{2}{x}^{\mathrm{3}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{8}}{dx}\:. \\ $$

Question Number 48042 Answers: 0 Comments: 1

find the value of ∫_(−∞) ^(+∞) ((2x+1)/((x^2 +i)(x^2 +4)))dx (i^2 =−1)

$${find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{i}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}\:\:\:\left({i}^{\mathrm{2}} =−\mathrm{1}\right) \\ $$

Question Number 48040 Answers: 0 Comments: 1

let f(α)=∫_(−∞) ^(+∞) ((xsin(αx))/((1+x^2 )^2 ))dx calculate f(α) and f^′ (α).(α from R) .

$${let}\:{f}\left(\alpha\right)=\int_{−\infty} ^{+\infty} \:\:\frac{{xsin}\left(\alpha{x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$${calculate}\:{f}\left(\alpha\right)\:{and}\:{f}^{'} \left(\alpha\right).\left(\alpha\:{from}\:{R}\right)\:. \\ $$

Question Number 48027 Answers: 2 Comments: 1

Question Number 47985 Answers: 1 Comments: 3

calculate I=∫_0 ^1 (√(1+2(√(x−x^2 ))))dx and J =∫_0 ^1 (√(1−2(√(x−x^2 ))))dx

$${calculate}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }}{dx}\:\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }}{dx} \\ $$

Question Number 47967 Answers: 1 Comments: 0

A particle moves in a linear scare such that acceleration after t seconds is a ms^(−2) where a= 2t^2 + t.If its initial velocity was 3ms^(−1) find an expression for S,the distance in meters traveled from start t seconds.

$${A}\:{particle}\:{moves}\:{in}\:{a}\:{linear}\:{scare}\:{such}\:{that}\:{acceleration} \\ $$$${after}\:{t}\:{seconds}\:{is}\:{a}\:{ms}^{−\mathrm{2}} \:{where}\:{a}=\:\mathrm{2}{t}^{\mathrm{2}} +\:{t}.{If}\:{its}\:{initial}\: \\ $$$${velocity}\:{was}\:\mathrm{3}{ms}^{−\mathrm{1}} \:{find}\:{an}\:{expression}\:{for}\:{S},{the}\:{distance}\:{in}\:{meters} \\ $$$${traveled}\:{from}\:{start}\:{t}\:{seconds}. \\ $$

Question Number 47915 Answers: 2 Comments: 0

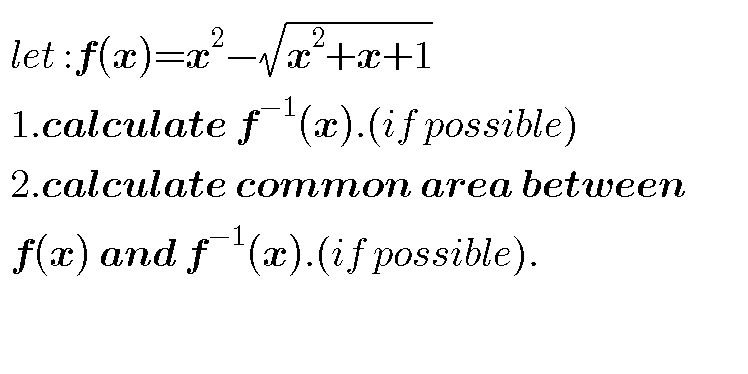
Question Number 47863 Answers: 0 Comments: 0

find ∫ (√(1−x^4 ))dx

$${find}\:\int\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$

Question Number 47852 Answers: 0 Comments: 1

1) find ∫ x arctan(x)dx 2) find the value of ∫_0 ^1 x arctan(x)dx

$$\left.\mathrm{1}\right)\:{find}\:\int\:{x}\:{arctan}\left({x}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{arctan}\left({x}\right){dx} \\ $$

Question Number 47851 Answers: 2 Comments: 3

let f(x)=x+1+(√x) and g(x)=x+1−(√x) find ∫ ((f(x))/(g(x)))dx and ((∫f(x)dx)/(∫g(x)dx)) .

$${let}\:\:{f}\left({x}\right)={x}+\mathrm{1}+\sqrt{{x}}\:{and}\:{g}\left({x}\right)={x}+\mathrm{1}−\sqrt{{x}} \\ $$$${find}\:\int\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}{dx}\:\:{and}\:\:\frac{\int{f}\left({x}\right){dx}}{\int{g}\left({x}\right){dx}}\:. \\ $$

Question Number 47850 Answers: 1 Comments: 2

calculate A_p =∫_0 ^1 ((x^p −1)/(ln(x)))dx with p>0.

$${calculate}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{p}} −\mathrm{1}}{{ln}\left({x}\right)}{dx}\:{with}\:{p}>\mathrm{0}. \\ $$

Question Number 47737 Answers: 1 Comments: 0

I = ∫_0 ^( L/2) ((Rz^2 )/((d^2 +z^2 )(√(d^2 +z^2 −R^2 )))) dz Find I .

$$\:\:{I}\:=\:\int_{\mathrm{0}} ^{\:\:{L}/\mathrm{2}} \frac{{Rz}^{\mathrm{2}} }{\left({d}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\sqrt{{d}^{\mathrm{2}} +{z}^{\mathrm{2}} −{R}^{\mathrm{2}} }}\:{dz} \\ $$$$\:{Find}\:{I}\:. \\ $$

Question Number 47720 Answers: 2 Comments: 0

find ∫ ln(1+x^3 )dx

$${find}\:\int\:{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$

Question Number 47677 Answers: 0 Comments: 3

∫x^(x ) dx=

$$\int\mathrm{x}^{\mathrm{x}\:} \mathrm{dx}= \\ $$

Question Number 47675 Answers: 2 Comments: 0

A particle of mass 4kg was at rest a a point of position vector i +4j. A force F was applied to it and it moved at a velocity of (3i + 7j)ms^(−1) after a time of 5seconds. Find a) the magnitude of F b) The speed at which it moves,Hence, c) The distance it covered.

$${A}\:{particle}\:{of}\:{mass}\:\mathrm{4}{kg}\:{was}\:{at}\:{rest}\:{a}\:{a}\:{point}\:{of}\:{position}\:{vector} \\ $$$${i}\:+\mathrm{4}{j}.\:{A}\:{force}\:{F}\:{was}\:{applied}\:{to}\:{it}\:{and}\:{it}\:{moved}\:{at}\:{a}\:{velocity} \\ $$$${of}\:\left(\mathrm{3}{i}\:+\:\mathrm{7}{j}\right){ms}^{−\mathrm{1}} \:\:\:{after}\:{a}\:{time}\:{of}\:\:\mathrm{5}{seconds}.\:{Find}\: \\ $$$$\left.{a}\right)\:{the}\:{magnitude}\:{of}\:{F} \\ $$$$\left.{b}\right)\:{The}\:{speed}\:{at}\:{which}\:{it}\:{moves},{Hence}, \\ $$$$\left.{c}\right)\:{The}\:{distance}\:{it}\:{covered}. \\ $$$$ \\ $$$$ \\ $$

Question Number 47651 Answers: 1 Comments: 1

calculate A_n =∫_0 ^1 sin([nx])e^(−2x) dx with n integr natural .

$${calculate}\:\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{sin}\left(\left[{nx}\right]\right){e}^{−\mathrm{2}{x}} {dx}\:{with}\:{n} \\ $$$${integr}\:{natural}\:. \\ $$

Question Number 47595 Answers: 0 Comments: 3

Question Number 47566 Answers: 2 Comments: 0

∫sin51x(sinx)^(49) dx

$$\int{sin}\mathrm{51}{x}\left({sinx}\right)^{\mathrm{49}} {dx} \\ $$

Question Number 47527 Answers: 0 Comments: 0

Pg 258 Pg 259 Pg 260 Pg 261 Pg 262 Pg 263 Pg 264 Pg 265 Pg 266 Pg 267

Contact: info@tinkutara.com