Question and Answers Forum

IntegrationQuestion and Answers: Page 257

Question Number 52484 Answers: 2 Comments: 0

∫ ((cos x − x sin x)/(x cos x)) dx

$$\int\:\:\frac{\mathrm{cos}\:\mathrm{x}\:−\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\:\:\mathrm{dx} \\ $$

Question Number 52482 Answers: 0 Comments: 2

find the value or ∫_0 ^∞ ((arctan(x^2 ))/(1+x^4 ))dx .

$${find}\:{the}\:{value}\:{or}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\:. \\ $$

Question Number 52459 Answers: 0 Comments: 2

let f(α)=∫_0 ^1 ((ln(1+iαx))/(1+x^2 ))dx 1)determine a explicit form of f(α) 2) calculate ∫_0 ^1 ((ln(1+ix))/(1+x^2 ))dx and ∫_0 ^1 ((ln(1+2ix))/(1+x^2 ))dx.

$${let}\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{i}\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{1}\right){determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left(\alpha\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{ix}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{ix}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}. \\ $$

Question Number 52418 Answers: 0 Comments: 1

find the value of ∫_0 ^∞ ((arctan(x))/(1+x^4 )) dx

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$

Question Number 52363 Answers: 2 Comments: 0

integrate ((sin^2 xcos^2 x )/(sin^3 x+cos^3 x))dx

$${integrate}\:\frac{\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}\:}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}}{dx} \\ $$

Question Number 52356 Answers: 1 Comments: 8

Question Number 52233 Answers: 3 Comments: 0

please can you help me with this caculus: ∫(1/(cos^2 x)) dx

$${please}\:{can}\:{you}\:{help}\:{me}\:{with}\:{this}\: \\ $$$${caculus}:\:\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$

Question Number 52197 Answers: 1 Comments: 0

calculate ∫_(π/4) ^(π/3) ((cosx −sinx)/(2 +sin(2x)))dx

$${calculate}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{cosx}\:−{sinx}}{\mathrm{2}\:+{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$ \\ $$

Question Number 52164 Answers: 2 Comments: 4

find: ∫_0 ^Π (cos^6 θ −cos^4 θ) dθ plase help me in cinding this And also explain if possible

$${find}: \\ $$$$\underset{\mathrm{0}} {\overset{\Pi} {\int}}\left({cos}^{\mathrm{6}} \theta\:−\mathrm{cos}\:^{\mathrm{4}} \theta\right)\:{d}\theta \\ $$$${plase}\:{help}\:{me}\:{in}\:{cinding}\:{this}\:{And}\:{also} \\ $$$${explain}\:{if}\:{possible} \\ $$

Question Number 52089 Answers: 0 Comments: 0

Question Number 51998 Answers: 0 Comments: 1

let U ={(x,y)∈R^2 / 1≤x^2 +2y^2 ≤3} calculate ∫∫_U ((x−y)/(x^2 +y^2 ))dxdxy

$${let}\:{U}\:=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:\mathrm{1}\leqslant{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \leqslant\mathrm{3}\right\} \\ $$$${calculate}\:\int\int_{{U}} \:\:\:\:\frac{{x}−{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdxy} \\ $$

Question Number 51997 Answers: 1 Comments: 2

let f(x)=∫_0 ^(π/2) (dt/(1+xsint)) with x>−1 1) calculate f(o) ,f(1) and f(2) 2) give f at form of function

$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{xsint}}\:\:{with}\:{x}>−\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({o}\right)\:,{f}\left(\mathrm{1}\right)\:{and}\:{f}\left(\mathrm{2}\right) \\ $$$$\left.\mathrm{2}\right)\:{give}\:{f}\:{at}\:{form}\:{of}\:{function}\: \\ $$$$ \\ $$

Question Number 51995 Answers: 1 Comments: 0

let f defined on [0,1] by f(0)=0 and f(x)=(1/(2[(1/(2x))]+1)) calculate ∫_0 ^1 f(x)dx

$${let}\:\:{f}\:{defined}\:{on}\:\left[\mathrm{0},\mathrm{1}\right]\:{by}\:\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:{and}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}{x}}\right]+\mathrm{1}} \\ $$$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$

Question Number 51994 Answers: 0 Comments: 1

let D_n = {(x,y)∈R^2 /(x,y)∈[(1/n) ,n[ } 1) find the value of ∫∫_D_n e^(−x^2 −y^2 ) dxdy 2) calculate ∫_0 ^(+∞) e^(−x^2 ) dx .

$${let}\:{D}_{{n}} =\:\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:\:/\left({x},{y}\right)\in\left[\frac{\mathrm{1}}{{n}}\:,{n}\left[\:\right\}\right.\right. \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\int\int_{{D}_{{n}} } \:\:\:\:\:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:. \\ $$

Question Number 51993 Answers: 0 Comments: 0

find A_n (x)=∫_0 ^1 (1−t^2 )^n cos(tx)dt

$${find}\:{A}_{{n}} \left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} {cos}\left({tx}\right){dt} \\ $$

Question Number 51992 Answers: 0 Comments: 0

find lim_(x→0) ∫_x ^(2x) (t/(ln(1+t^2 )))dt

$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\int_{{x}} ^{\mathrm{2}{x}} \:\:\:\:\frac{{t}}{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$

Question Number 51991 Answers: 0 Comments: 1

find f(a) =∫ (dx/((√(1+ax^2 ))+(√(1−ax^2 )))) with a>0

$${find}\:{f}\left({a}\right)\:=\int\:\:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{ax}^{\mathrm{2}} }}\:\:{with}\:{a}>\mathrm{0} \\ $$

Question Number 51990 Answers: 1 Comments: 0

calculate ∫_(1/2) ^1 x arctan((√(1−x^2 )))dx

$${calculate}\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:{x}\:{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx} \\ $$

Question Number 51989 Answers: 1 Comments: 0

calculate ∫_(π/4) ^(π/3) ((sinx)/(1+sin^2 x))dx

$${calculate}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\frac{{sinx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}{dx} \\ $$

Question Number 51988 Answers: 0 Comments: 0

let f(a) =∫ (√(a^2 −x^4 ))dx 1) determine a explicit form of f(a) 2) find ∫ (dx/(√(a^2 −x^4 ))) a>0

$${let}\:{f}\left({a}\right)\:=\int\:\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{4}} }{dx} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int\:\:\:\:\frac{{dx}}{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{4}} }} \\ $$$${a}>\mathrm{0} \\ $$

Question Number 51987 Answers: 1 Comments: 1

calculate ∫_0 ^(1/2) (√(1−x^4 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$

Question Number 51959 Answers: 0 Comments: 4

Question Number 51910 Answers: 0 Comments: 4

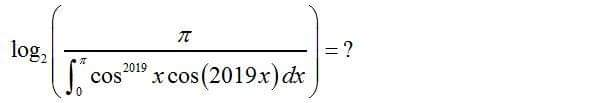
Question Number 51876 Answers: 1 Comments: 2

Question Number 51841 Answers: 0 Comments: 2

Question Number 51834 Answers: 0 Comments: 1

calculatef(a)= ∫_0 ^∞ ((ln(1+at^2 ))/(1+t^4 ))dt with a>0. 2)find the value of ∫_0 ^∞ ((ln(3+t^2 ))/(1+t^4 ))dt.

$${calculatef}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}+{at}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{4}} }{dt}\:\:{with}\:{a}>\mathrm{0}. \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{3}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{4}} }{dt}. \\ $$

Pg 252 Pg 253 Pg 254 Pg 255 Pg 256 Pg 257 Pg 258 Pg 259 Pg 260 Pg 261

Contact: info@tinkutara.com