Question and Answers Forum

IntegrationQuestion and Answers: Page 247

Question Number 59163 Answers: 0 Comments: 0

calculate A_n =∫∫_W_n ((1−(√(x^2 +y^2 )))/(1+(√(x^2 +y^2 )))) dxdy with W_n =](1/n),n[^2 2) find lim_(n→+∞) A_n

$$\left.{calculate}\:{A}_{{n}} =\int\int_{{W}_{{n}} } \:\:\:\frac{\mathrm{1}−\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\:{dxdy}\:\:\:{with}\:{W}_{{n}} \:=\right]\frac{\mathrm{1}}{{n}},{n}\left[^{\mathrm{2}} \right. \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$

Question Number 59162 Answers: 0 Comments: 0

calculate ∫∫_D (√(x^2 −y^2 ))xy dxdy with D ={(x,y)∈ R^2 /0≤y≤1 and 2 ≤x ≤5 }

$${calculate}\:\:\int\int_{{D}} \:\:\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{xy}\:{dxdy}\:\:{with} \\ $$$${D}\:=\left\{\left({x},{y}\right)\in\:{R}^{\mathrm{2}} \:\:\:/\mathrm{0}\leqslant{y}\leqslant\mathrm{1}\:\:{and}\:\:\mathrm{2}\:\leqslant{x}\:\leqslant\mathrm{5}\:\right\} \\ $$

Question Number 59161 Answers: 0 Comments: 0

calculatef(a)= ∫_0 ^∞ ((ln(a^2 +x^2 ))/(a^2 +x^2 ))dx with >0 1) calculate ∫_0 ^∞ ((ln(2+x^2 ))/(2+x^2 ))dx and ∫_0 ^∞ ((ln(3+x^2 ))/(3+x^2 )) dx .

$${calculatef}\left({a}\right)=\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}\:\:\:{with}\:>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}{\mathrm{2}+{x}^{\mathrm{2}} }{dx}\:\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right)}{\mathrm{3}+{x}^{\mathrm{2}} }\:{dx}\:. \\ $$

Question Number 59052 Answers: 0 Comments: 0

let f(x) =∫_0 ^(π/2) ln(cosθ +xsinθ)dθ with x fromR 1) determine a explicit form for f(x) 2) calculate ∫_0 ^(π/2) ln(cosθ +sinθ) dθ and ∫_0 ^(π/2) ln(cosθ +2sinθ)dθ .

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\theta\:+{xsin}\theta\right){d}\theta\:\:\:{with}\:{x}\:{fromR} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:\:{for}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\theta\:+{sin}\theta\right)\:{d}\theta\:\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\theta\:+\mathrm{2}{sin}\theta\right){d}\theta\:. \\ $$

Question Number 59050 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((arctan(x^2 ))/(1+x^2 )) dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\: \\ $$

Question Number 59040 Answers: 3 Comments: 0

1) ∫_0 ^( (π/4)) ((sin x+cos x)/(cos^2 x+sin^4 x))dx = ?

$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{4}} {x}}{dx}\:=\:? \\ $$

Question Number 59012 Answers: 3 Comments: 0

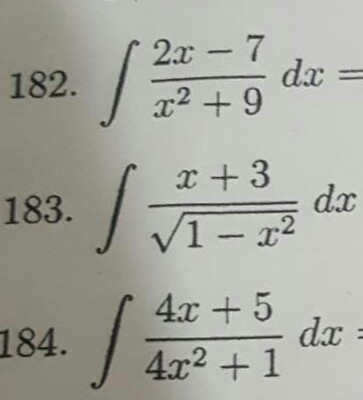
Question Number 58940 Answers: 1 Comments: 3

e^(i∫_(−2) ^2 (x^2 sinx+(√(1−(x^2 /4))))dx) +lim_(x→2) ((∫_2 ^x log(x+8)dx)/(x−2))=?

$${e}^{{i}\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} {sinx}+\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right){dx}} +\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\int_{\mathrm{2}} ^{{x}} {log}\left({x}+\mathrm{8}\right){dx}}{{x}−\mathrm{2}}=? \\ $$

Question Number 58937 Answers: 0 Comments: 2

∫_0 ^2 lim_((1/n)→0) (((2−x)(x+x^n ))/(1+x^n ))dx= ?

$$\int_{\mathrm{0}} ^{\mathrm{2}} \underset{\frac{\mathrm{1}}{{n}}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}−{x}\right)\left({x}+{x}^{{n}} \right)}{\mathrm{1}+{x}^{{n}} }{dx}=\:? \\ $$

Question Number 58791 Answers: 1 Comments: 0

Show that: ∫_( 0) ^( ∞) ((sin(x))/x) = (π/2)

$$\:\boldsymbol{\mathrm{Show}}\:\boldsymbol{\mathrm{that}}:\:\:\:\:\:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\infty} \:\:\:\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\:\:\:=\:\:\frac{\pi}{\mathrm{2}} \\ $$

Question Number 58774 Answers: 0 Comments: 3

let f(x) =∫_(π/3) ^(π/2) (dθ/(1+xtanθ)) with x real 1) find a explicit form for f(x) 2) determine also g(x) =∫_(π/3) ^(π/2) ((tanθ)/((1+xtanθ)^2 )) dθ 3) let U_n (x) =f^((n)) (x) give U_n (x) at form of integral. 4) calculate ∫_(π/3) ^(π/2) (dθ/(1+2tanθ)) and ∫_(π/3) ^(π/2) ((tanθ dθ)/((1+2tanθ)^2 ))

$${let}\:{f}\left({x}\right)\:=\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{d}\theta}{\mathrm{1}+{xtan}\theta}\:\:\:{with}\:{x}\:{real} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{for}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{also}\:{g}\left({x}\right)\:=\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{tan}\theta}{\left(\mathrm{1}+{xtan}\theta\right)^{\mathrm{2}} }\:{d}\theta \\ $$$$\left.\mathrm{3}\right)\:{let}\:{U}_{{n}} \left({x}\right)\:={f}^{\left({n}\right)} \left({x}\right)\:\:{give}\:{U}_{{n}} \left({x}\right)\:{at}\:{form}\:{of}\:{integral}. \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\mathrm{1}+\mathrm{2}{tan}\theta}\:\:{and}\:\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{tan}\theta\:{d}\theta}{\left(\mathrm{1}+\mathrm{2}{tan}\theta\right)^{\mathrm{2}} } \\ $$

Question Number 58770 Answers: 2 Comments: 1

find the value of integrals I =∫_0 ^∞ (dx/((x^2 +1)^3 )) , J =∫_0 ^∞ (dx/((x^2 +1)^5 ))

$${find}\:{the}\:{value}\:{of}\:{integrals} \\ $$$$\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:\:\:,\:{J}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{5}} } \\ $$

Question Number 58717 Answers: 1 Comments: 1

Question Number 58648 Answers: 2 Comments: 4

Question Number 58639 Answers: 1 Comments: 0

Question Number 58627 Answers: 1 Comments: 3

Question Number 58626 Answers: 1 Comments: 1

Question Number 58595 Answers: 1 Comments: 0

Question Number 58488 Answers: 0 Comments: 2

let f(x) =∫ (dt/(x +cost +cos(2t))) (x real) 1) find a explicit form of f(x) 2)determine also ∫ (dt/((x+cost +cos(2t))^2 )) 3) find ∫ (dt/(1+cos(t)+cos(2t))) and ∫ (dt/((3 +cos(t)+cos(2t))^2 ))

$${let}\:{f}\left({x}\right)\:=\int\:\:\:\frac{{dt}}{{x}\:+{cost}\:+{cos}\left(\mathrm{2}{t}\right)}\:\:\left({x}\:{real}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){determine}\:{also}\:\int\:\:\frac{{dt}}{\left({x}+{cost}\:+{cos}\left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:{find}\:\int\:\:\:\frac{{dt}}{\mathrm{1}+{cos}\left({t}\right)+{cos}\left(\mathrm{2}{t}\right)}\:{and} \\ $$$$\int\:\:\:\frac{{dt}}{\left(\mathrm{3}\:+{cos}\left({t}\right)+{cos}\left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} } \\ $$

Question Number 58487 Answers: 0 Comments: 3

let f(x) =∫_(π/4) ^(π/3) (dt/(2+xsint)) 1) find a explicit form of f(x) 2)determine also g(x)=∫_(π/4) ^(π/3) ((sint)/((2+xsint)^2 ))dt 3) find the value of ∫_(π/4) ^(π/3) (dt/(2+3sint)) and ∫_(π/4) ^(π/3) ((sint)/((2+3sint)^2 ))dt

$${let}\:{f}\left({x}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\frac{{dt}}{\mathrm{2}+{xsint}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){determine}\:{also}\:{g}\left({x}\right)=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\frac{{sint}}{\left(\mathrm{2}+{xsint}\right)^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{{dt}}{\mathrm{2}+\mathrm{3}{sint}} \\ $$$${and}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\frac{{sint}}{\left(\mathrm{2}+\mathrm{3}{sint}\right)^{\mathrm{2}} }{dt} \\ $$

Question Number 58478 Answers: 2 Comments: 1

{1} ∫((x^2 −2)/(x^4 +8x^2 +4)) dx = ? {2} Shortest distance between the parabolas y^2 =4x and y^2 =2x−6 is ?

$$\left\{\mathrm{1}\right\}\:\:\:\int\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{4}}\:{dx}\:=\:? \\ $$$$\left\{\mathrm{2}\right\}\:\:{Shortest}\:{distance}\:{between}\:{the} \\ $$$${parabolas}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:{and}\:{y}^{\mathrm{2}} =\mathrm{2}{x}−\mathrm{6}\:{is}\:? \\ $$

Question Number 58319 Answers: 1 Comments: 0

∫x^n (lnx)^n dx

$$\int{x}^{{n}} \left(\mathrm{ln}{x}\right)^{{n}} {dx} \\ $$

Question Number 58299 Answers: 1 Comments: 1

find ∫ (dx/((x^2 +x+1)^(3/2) ))

$${find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Question Number 58259 Answers: 4 Comments: 4

a .∫ (dx/(2sin^2 x+3tg^2 x))=? b .∫(( 1+(x)^(1/3) )/(1+(√x)+(x)^(1/3) +(x)^(1/6) ))dx=? c .∫ ((cosx)/(1+cos2x))dx=? d .∫ ((sin^2 x)/((√2)+(√3).cos^2 x))dx=?

Question Number 58250 Answers: 1 Comments: 0

∫_( 0) ^( 1) (((3x^3 − x^2 + 2x − 4)/(√(x^2 − 3x + 2)))) dx

$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\:\left(\frac{\mathrm{3x}^{\mathrm{3}} \:−\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{2x}\:−\:\mathrm{4}}{\sqrt{\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{2}}}\right)\:\mathrm{dx} \\ $$

Question Number 58249 Answers: 0 Comments: 0

I_n ^ =∫_0 ^(π/2) cos^n xcos(nx)dx then show that I_1 ,I_2 ,I_3 ....are in G.P

$$\overset{} {{I}}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{n}} {xcos}\left({nx}\right){dx} \\ $$$${then}\:{show}\:{that}\:{I}_{\mathrm{1}} ,{I}_{\mathrm{2}} ,{I}_{\mathrm{3}} ....{are}\:{in}\:{G}.{P} \\ $$

Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251

Contact: info@tinkutara.com