
IntegrationQuestion and Answers: Page 244
Question Number 60595 Answers: 0 Comments: 2
Question Number 60496 Answers: 0 Comments: 1
Question Number 60495 Answers: 0 Comments: 0
Question Number 60494 Answers: 1 Comments: 1
$${find}\:\int\:\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}}{dx} \\ $$
Question Number 60481 Answers: 0 Comments: 0
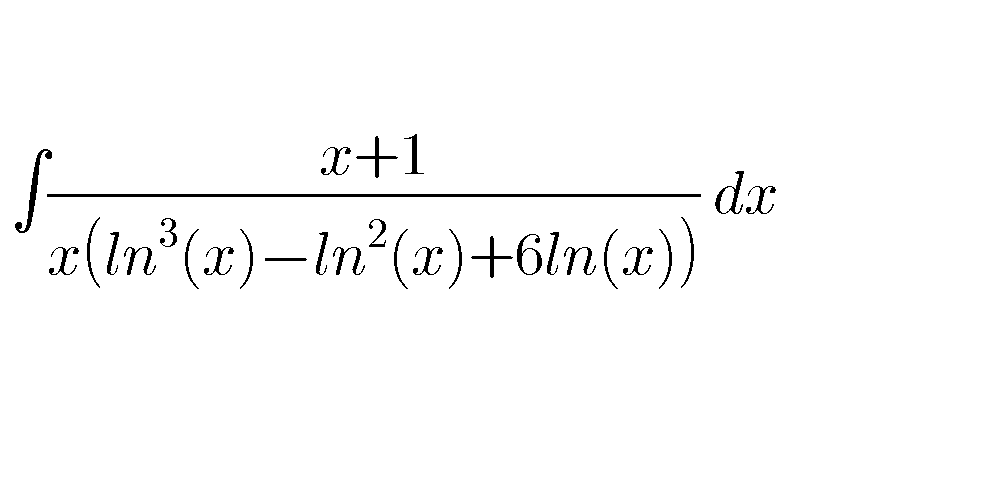
Question Number 60424 Answers: 0 Comments: 2
Question Number 60413 Answers: 1 Comments: 4

Question Number 60384 Answers: 0 Comments: 0
$$\int{e}^{{coth}^{−\mathrm{1}} \left({x}\right)} \:{dx}\: \\ $$
Question Number 60376 Answers: 1 Comments: 2
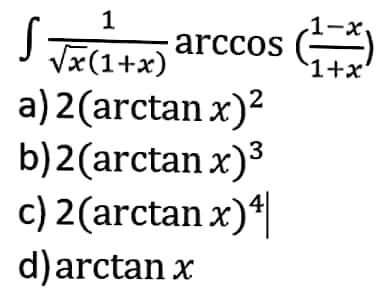
Question Number 60335 Answers: 0 Comments: 0
Question Number 60346 Answers: 0 Comments: 1
$$\int{x}\mathrm{sec}\:^{\mathrm{3}} {xdx} \\ $$$${please}\:{help} \\ $$
Question Number 60320 Answers: 0 Comments: 1

Question Number 60319 Answers: 0 Comments: 0

Question Number 60318 Answers: 0 Comments: 2
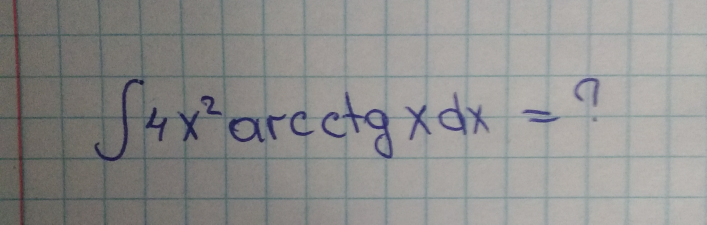
Question Number 60311 Answers: 1 Comments: 2
$$\int\frac{{dx}}{\sqrt{{sec}\:{h}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}}\:{dx} \\ $$
Question Number 60264 Answers: 0 Comments: 0
Question Number 60263 Answers: 0 Comments: 1
Question Number 60234 Answers: 1 Comments: 0
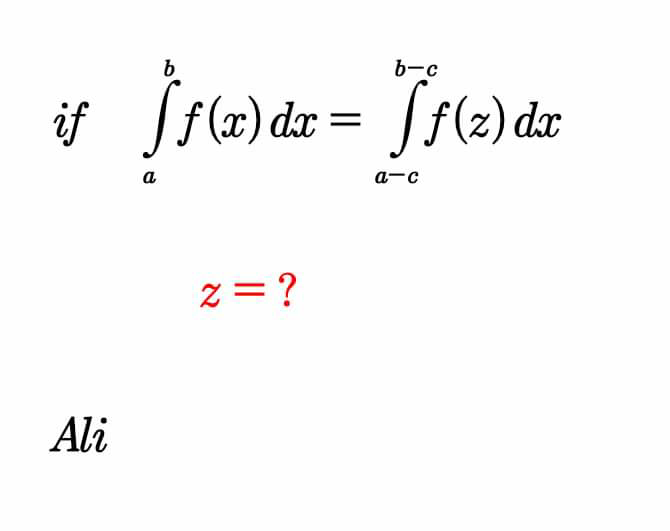
Question Number 60170 Answers: 0 Comments: 0
Question Number 60050 Answers: 1 Comments: 1
Question Number 60036 Answers: 1 Comments: 0

Question Number 60027 Answers: 1 Comments: 0
Question Number 60025 Answers: 0 Comments: 0

Question Number 59999 Answers: 0 Comments: 0
Question Number 59998 Answers: 1 Comments: 3
$${find}\:\int\:\frac{{dx}}{{acosx}\:+{bsinx}}\:\:{with}\:{a}\:{and}\:{b}\:{reals} \\ $$
Question Number 59991 Answers: 0 Comments: 2

Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248
