Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 243

Question Number 60716 Answers: 1 Comments: 1

Question Number 60692 Answers: 0 Comments: 0

find ∫ arctan(2cosx)dx

$${find}\:\:\int\:\:{arctan}\left(\mathrm{2}{cosx}\right){dx}\: \\ $$

Question Number 60691 Answers: 0 Comments: 1

calculate f(a) = ∫ (1−(a/x^2 )) arctan(x+(a/x))dx with a real .

$${calculate}\:{f}\left({a}\right)\:=\:\int\:\:\:\left(\mathrm{1}−\frac{{a}}{{x}^{\mathrm{2}} }\right)\:{arctan}\left({x}+\frac{{a}}{{x}}\right){dx}\:\:\:{with}\:{a}\:{real}\:. \\ $$

Question Number 60690 Answers: 0 Comments: 0

find ∫ (x+3)(√((1−x^2 )/(1+x^2 )))dx

$${find}\:\int\:\left({x}+\mathrm{3}\right)\sqrt{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}{dx}\: \\ $$

Question Number 60688 Answers: 0 Comments: 0

find ∫ e^(−x) (√((3−x)/(3+x)))dx

$${find}\:\int\:\:\:{e}^{−{x}} \sqrt{\frac{\mathrm{3}−{x}}{\mathrm{3}+{x}}}{dx} \\ $$

Question Number 60687 Answers: 1 Comments: 2

calculate ∫ (((√(1+x^2 ))−2x)/((√(1+x^2 )) +2x)) dx

$${calculate}\:\:\int\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{2}{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\mathrm{2}{x}}\:{dx} \\ $$

Question Number 60685 Answers: 1 Comments: 1

find I_n =∫_0 ^(π/2) ((1−cos(nx))/(sin^2 (nx)))dx

$${find}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{cos}\left({nx}\right)}{{sin}^{\mathrm{2}} \left({nx}\right)}{dx}\: \\ $$

Question Number 60686 Answers: 0 Comments: 0

let f(x) =cos(2x) ,2π periodic , developp f at fourier serie

$${let}\:{f}\left({x}\right)\:={cos}\left(\mathrm{2}{x}\right)\:\:\:\:,\mathrm{2}\pi\:{periodic}\:,\:\:{developp}\:{f}\:{at}\:{fourier}\:{serie} \\ $$

Question Number 60683 Answers: 0 Comments: 0

find A_n =∫_0 ^(π/4) sin^n xdx with n integr natural .

$${find}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{{n}} {xdx}\:\:\:\:{with}\:{n}\:{integr}\:{natural}\:. \\ $$

Question Number 60681 Answers: 0 Comments: 1

calculate L(e^(−2x) sin(αx)) α real and L laplace transform

$${calculate}\:\:{L}\left({e}^{−\mathrm{2}{x}} {sin}\left(\alpha{x}\right)\right)\:\:\:\:\alpha\:{real}\:\:\:{and}\:{L}\:{laplace}\:{transform} \\ $$

Question Number 60680 Answers: 0 Comments: 2

study the integral ∫_0 ^1 (x/(ln(1−x)))dx

$${study}\:{the}\:{integral}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}}{{ln}\left(\mathrm{1}−{x}\right)}{dx} \\ $$

Question Number 60679 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((ln(1+e^(−x^2 ) ))/(x^2 +4)) dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:{dx} \\ $$

Question Number 60678 Answers: 0 Comments: 3

calculate ∫_0 ^1 ((ln(1−x^2 ))/x) dx

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}\:{dx} \\ $$

Question Number 60670 Answers: 1 Comments: 2

Question Number 60675 Answers: 0 Comments: 0

∫_0 ^(π/2) ln[((ln^2 (sin(x)))/(π^2 +ln^2 (sinx)))]((ln(cos(x)))/(tan(x)))dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left[\frac{{ln}^{\mathrm{2}} \left({sin}\left({x}\right)\right)}{\pi^{\mathrm{2}} +{ln}^{\mathrm{2}} \left({sinx}\right)}\right]\frac{{ln}\left({cos}\left({x}\right)\right)}{{tan}\left({x}\right)}{dx} \\ $$

Question Number 60662 Answers: 0 Comments: 0

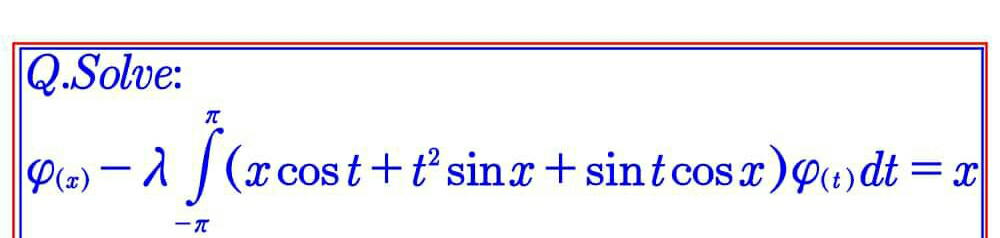
Question Number 60659 Answers: 1 Comments: 1

find ∫_0 ^1 ln(x)ln(1−x^2 )dx

$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 60658 Answers: 0 Comments: 1

calculate ∫_0 ^1 ln(x)ln(1−x)ln(1−x^2 )dx

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 60637 Answers: 1 Comments: 1

Question Number 60623 Answers: 0 Comments: 0

What are all intregal methods that exist like trigonometry sub. Gaussian method feyman method ?

$$\mathrm{W}{hat}\:{are}\:{all}\:{intregal}\:{methods}\:{that}\:{exist} \\ $$$${like}\:{trigonometry}\:{sub}.\:{Gaussian}\:{method}\:{feyman}\:{method}\:? \\ $$$$ \\ $$$$ \\ $$

Question Number 60621 Answers: 0 Comments: 5

if π is rational then there exists a I_n =(v^(2n) /(n!))∫_0 ^π x^n (x−π)^n sin(x)dx can someone give a easier way to expaned this

$${if}\:\pi\:{is}\:{rational}\:{then}\:{there} \\ $$$${exists}\:{a}\:{I}_{{n}} =\frac{{v}^{\mathrm{2}{n}} }{{n}!}\underset{\mathrm{0}} {\overset{\pi} {\int}}{x}^{{n}} \left({x}−\pi\right)^{{n}} {sin}\left({x}\right){dx} \\ $$$${can}\:{someone}\:{give}\:{a}\:{easier}\:{way}\:{to}\:{expaned}\:{this} \\ $$

Question Number 60631 Answers: 0 Comments: 0

prove that∫_(−∞) ^∞ x^5 e^(−x^2 ) sin(x^3 ) dx=0.25474

$$\mathrm{prove}\:\mathrm{that}\underset{−\infty} {\overset{\infty} {\int}}\mathrm{x}^{\mathrm{5}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{sin}\left(\mathrm{x}^{\mathrm{3}} \right)\:\mathrm{dx}=\mathrm{0}.\mathrm{25474} \\ $$

Question Number 60586 Answers: 0 Comments: 1

find ∫_0 ^1 ((ln^2 (x))/((1−x^2 )^2 ))dx

$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$

Question Number 60534 Answers: 0 Comments: 1

Question Number 60506 Answers: 0 Comments: 1

calculate ∫∫_W ((√(2x^2 +3y^2 ))/(x+y)) dxdy with W ={(x,y)∈R^2 / 0<x<1 and 0<y<1.

$${calculate}\:\int\int_{{W}} \:\:\:\:\:\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}{y}^{\mathrm{2}} }}{{x}+{y}}\:{dxdy} \\ $$$${with}\:{W}\:=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:\mathrm{0}<{x}<\mathrm{1}\:{and}\:\mathrm{0}<{y}<\mathrm{1}.\right. \\ $$

Question Number 60498 Answers: 0 Comments: 4

let f(t) =∫_0 ^3 (√(t +x +x^2 ))dx with t ≥(1/4) 1) find a explicit form of f(t) 2) find also g(t) = ∫_0 ^3 (dx/(√(t+x +x^2 ))) 3) calculate ∫_0 ^3 (√(1+x+x^2 ))dx , ∫_0 ^3 (√(2 +x+x^2 ))dx ∫_0 ^3 (dx/(√(2+x +x^2 ))) .

$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{{t}\:+{x}\:+{x}^{\mathrm{2}} }{dx}\:\:{with}\:{t}\:\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({t}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{also}\:{g}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\sqrt{{t}+{x}\:+{x}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{3}} \:\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\:,\:\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{2}\:+{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\sqrt{\mathrm{2}+{x}\:+{x}^{\mathrm{2}} }}\:\:. \\ $$

Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247

Terms of Service

Contact: info@tinkutara.com