Question and Answers Forum

IntegrationQuestion and Answers: Page 235

Question Number 64065 Answers: 0 Comments: 3

calculate ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 64037 Answers: 0 Comments: 1

reduction formulas for n∈N, some n>0, some n>1 ∫sin^n x dx=−(1/n)cos x sin^(n−1) x +((n−1)/n)∫sin^(n−2) x dx ∫cos^n x dx=(1/n)sin x cos^(n−1) x +((n−1)/n)∫cos^(n−2) x dx ∫tan^n x dx=(1/(n−1))tan^(n−1) x −∫tan^(n−2) x dx ∫sec^n x dx=(1/(n−1))tan x sec^(n−2) x +((n−2)/(n−1))∫sec^(n−2) x dx ∫csc^n x dx=−(1/(n−1))cot x csc^(n−2) x +((n−2)/(n−1))∫csc^(n−2) x dx ∫cot^n x dx=−(1/(n−1))cot^(n−1) x −∫cot^(n−2) x dx

Question Number 63976 Answers: 0 Comments: 3

∫secxdx ?

$$\int{secxdx}\:\:\:\:? \\ $$

Question Number 63927 Answers: 0 Comments: 7

∫_0 ^π (dx/((3+2cos x)^2 ))

$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\mathrm{3}+\mathrm{2}{cos}\:{x}\right)^{\mathrm{2}} } \\ $$

Question Number 63903 Answers: 0 Comments: 0

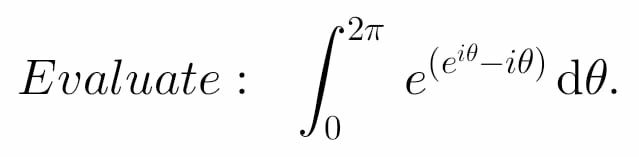
Question Number 63892 Answers: 0 Comments: 3

calculate A=∫_0 ^∞ (x^(2017) /(1+x^(2019) )) dx and B =∫_0 ^∞ (x^(2019) /(1+x^(2021) )) dx calculate the fraction (A/B)

$${calculate}\:{A}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2017}} }{\mathrm{1}+{x}^{\mathrm{2019}} }\:{dx}\:\:{and}\:{B}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2019}} }{\mathrm{1}+{x}^{\mathrm{2021}} }\:{dx} \\ $$$${calculate}\:{the}\:{fraction}\:\frac{{A}}{{B}} \\ $$

Question Number 63881 Answers: 0 Comments: 1

∫e^x /Lnxdx

$$\int{e}^{{x}} /{Lnxdx} \\ $$

Question Number 63883 Answers: 0 Comments: 1

∫ln(x)ln(1−x)ln(1−2x)dx

$$\int{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right){dx} \\ $$

Question Number 63852 Answers: 0 Comments: 0

prove that ∫_0 ^1 arctan(x) cot(((πx)/2)) dx = ((3 ln^2 (2))/(2π))+((lnπ ln2)/π)+∫_0 ^∞ ((ln(1+x^2 ))/(e^(2πx) +1)) dx

$${prove}\:{that} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {arctan}\left({x}\right)\:{cot}\left(\frac{\pi{x}}{\mathrm{2}}\right)\:{dx}\:=\:\frac{\mathrm{3}\:{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}\pi}+\frac{{ln}\pi\:{ln}\mathrm{2}}{\pi}+\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{e}^{\mathrm{2}\pi{x}} +\mathrm{1}}\:{dx} \\ $$

Question Number 63844 Answers: 3 Comments: 3

∫(1+4x+x^2 )^m dx

$$\int\left(\mathrm{1}+\mathrm{4}{x}+{x}^{\mathrm{2}} \right)^{{m}} {dx} \\ $$

Question Number 63822 Answers: 0 Comments: 1

find ∫ (x^2 +1)(√((x+1)/(x−2)))dx

$${find}\:\int\:\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}}{dx} \\ $$

Question Number 63782 Answers: 1 Comments: 4

let f(a) =∫_(−∞) ^(+∞) (dx/((a^2 +x^2 )^3 )) with a>0 1) calculate f(a) 2)calculste also g(a) =∫_(−∞) ^(+∞) (dx/((a^2 +x^2 )^4 )) 3) find the values of integrals ∫_0 ^∞ (dx/((x^2 +1)^3 )) ∫_0 ^∞ (dx/((x^2 +2)^4 ))

$${let}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right){calculste}\:{also}\:{g}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{values}\:{of}\:{integrals}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} } \\ $$

Question Number 63823 Answers: 0 Comments: 0

calculate ∫_(−∞) ^(+∞) ((3x^2 −1)/(x^4 −2x^2 +3))dx

$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$

Question Number 63748 Answers: 0 Comments: 0

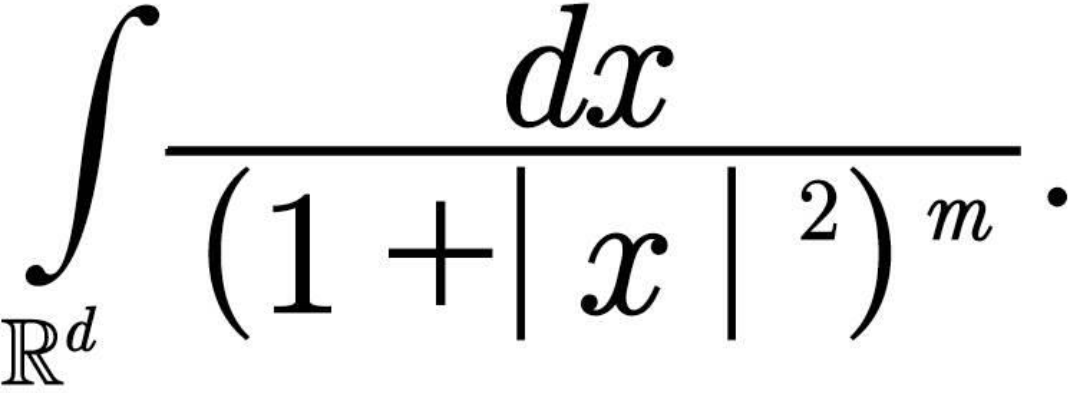
Question Number 63738 Answers: 0 Comments: 0

useful formula ======== ∀a∈R^+ :∀b ∈R: a sin x +b cos x =(√(a^2 +b^2 ))sin (x+arctan (b/a)) ∫(dx/(a sin x +b cos x))= =(1/(√(a^2 +b^2 )))∫(dx/(sin (x+arctan (b/a))))= [t=x+arctan (b/a) → dx=dt] (1/(√(a^2 +b^2 )))∫(dt/(sin t))=−(1/(√(a^2 +b^2 )))ln ((1/(sin t))+(1/(tan t))) = =−(1/(√(a^2 +b^2 )))ln ∣(((√(a^2 +b^2 ))−b sin x +a cos x)/(a sin x +b cos x))∣ +C

$$\mathrm{useful}\:\mathrm{formula} \\ $$$$======== \\ $$$$ \\ $$$$\forall{a}\in\mathbb{R}^{+} :\forall{b}\:\in\mathbb{R}:\:{a}\:\mathrm{sin}\:{x}\:+{b}\:\mathrm{cos}\:{x}\:=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\mathrm{sin}\:\left({x}+\mathrm{arctan}\:\frac{{b}}{{a}}\right) \\ $$$$\int\frac{{dx}}{{a}\:\mathrm{sin}\:{x}\:+{b}\:\mathrm{cos}\:{x}}= \\ $$$$=\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\int\frac{{dx}}{\mathrm{sin}\:\left({x}+\mathrm{arctan}\:\frac{{b}}{{a}}\right)}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{arctan}\:\frac{{b}}{{a}}\:\:\rightarrow\:{dx}={dt}\right] \\ $$$$\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\int\frac{{dt}}{\mathrm{sin}\:{t}}=−\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:{t}}+\frac{\mathrm{1}}{\mathrm{tan}\:{t}}\right)\:= \\ $$$$=−\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\mathrm{ln}\:\mid\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−{b}\:\mathrm{sin}\:{x}\:+{a}\:\mathrm{cos}\:{x}}{{a}\:\mathrm{sin}\:{x}\:+{b}\:\mathrm{cos}\:{x}}\mid\:+{C} \\ $$

Question Number 63722 Answers: 1 Comments: 6

1) calculate ∫ (x^2 −x+2)(√(x^2 −x+1))dx 2)find the value of ∫_0 ^1 (x^2 −x+2)(√(x^2 −x +1))dx .

$$\left.\mathrm{1}\right)\:{calculate}\:\int\:\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx}\:. \\ $$

Question Number 63721 Answers: 1 Comments: 2

calculate ∫ (dx/(√((x−1)(2−x))))

$${calculate}\:\int\:\:\frac{{dx}}{\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}} \\ $$

Question Number 63720 Answers: 1 Comments: 2

calculate ∫(√((x−3)(2−x)))dx

$${calculate}\:\int\sqrt{\left({x}−\mathrm{3}\right)\left(\mathrm{2}−{x}\right)}{dx} \\ $$

Question Number 63711 Answers: 1 Comments: 1

calculate ∫_0 ^π (dx/((√3)cosx +(√2)sinx))

$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{\sqrt{\mathrm{3}}{cosx}\:+\sqrt{\mathrm{2}}{sinx}} \\ $$

Question Number 63667 Answers: 0 Comments: 3

1) calculate ∫_0 ^(2π) (dt/(cost +x sint)) wih x from R. 2) calculate ∫_0 ^(2π) ((sint)/((cost +xsint)^2 ))dt 3) find[the value of ∫_0 ^(2π) (dt/(cos(2t)+2sin(2t)))

$$\left.\mathrm{1}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{cost}\:+{x}\:{sint}}\:\:\:{wih}\:{x}\:{from}\:{R}. \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{\left({cost}\:+{xsint}\right)^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{find}\left[{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{{cos}\left(\mathrm{2}{t}\right)+\mathrm{2}{sin}\left(\mathrm{2}{t}\right)}\right. \\ $$

Question Number 63666 Answers: 0 Comments: 3

calculate ∫_0 ^(2π) (dx/(2sinx +cosx))

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{2}{sinx}\:+{cosx}} \\ $$

Question Number 63664 Answers: 0 Comments: 6

let f(x)=∫_0 ^∞ (t^(a−1) /(x+t^n )) dt with 0<a<1 and x>0 and n≥2 1) determine a explicit form of f(x) 2) calculate g(x) =∫_0 ^∞ (t^(a−1) /((x+t^n )^2 )) dt 3) find f^((k)) (x) at form of integrals 4) calculate ∫_0 ^∞ (t^(a−1) /(9+t^2 )) dt and ∫_0 ^∞ (t^(a−1) /((9+t^2 )^2 )) 5) calculate U_n =∫_0 ^∞ (t^((1/n)−1) /(2^n +t^n )) dt and study the convergence of Σ U_n

$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{{x}+{t}^{{n}} }\:{dt}\:\:\:{with}\:\mathrm{0}<{a}<\mathrm{1}\:\:{and}\:\:{x}>\mathrm{0}\:{and}\:{n}\geqslant\mathrm{2} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\left({x}+{t}^{{n}} \right)^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{f}^{\left({k}\right)} \left({x}\right)\:{at}\:{form}\:{of}\:{integrals} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{9}+{t}^{\mathrm{2}} }\:{dt}\:\:\:\:{and}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{{a}−\mathrm{1}} }{\left(\mathrm{9}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{5}\right)\:{calculate}\:\:{U}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{2}^{{n}} \:+{t}^{{n}} }\:{dt}\:\:{and}\:{study}\:{the}\:{convergence}\:{of}\:\Sigma\:{U}_{{n}} \\ $$

Question Number 63662 Answers: 0 Comments: 1

let A_n =∫_0 ^∞ (x^(a−1) /(1+x^n ))dx with n integr and n≥2 and 0<a<1 1) calculate A_n 2) find the values of ∫_0 ^∞ (x^(a−1) /(1+x^2 ))dx and ∫_0 ^∞ (x^(a−1) /(1+x^3 ))dx 3)calculate ∫_0 ^∞ (dx/((√x)(1+x^4 ))) and ∫_0 ^∞ (dx/((^3 (√x^2 ))(1+x^4 )))

$$\:{let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{a}−\mathrm{1}} }{\mathrm{1}+{x}^{{n}} }{dx}\:\:{with}\:{n}\:{integr}\:{and}\:{n}\geqslant\mathrm{2}\:\:{and}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{values}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{a}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{a}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$\left.\mathrm{3}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\sqrt{{x}}\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left(^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} }\right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)} \\ $$

Question Number 63661 Answers: 0 Comments: 1

let 0<a<1 find the valueof ∫_0 ^∞ (t^(a−1) /(1+t^2 ))dt

$${let}\:\mathrm{0}<{a}<\mathrm{1}\:{find}\:{the}\:{valueof}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$

Question Number 63641 Answers: 0 Comments: 2

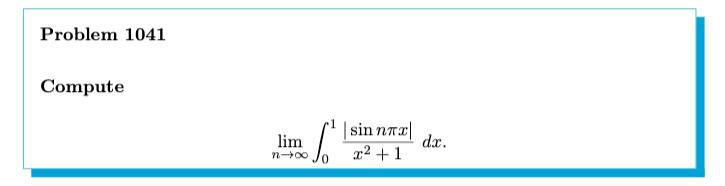
Question Number 63615 Answers: 0 Comments: 5

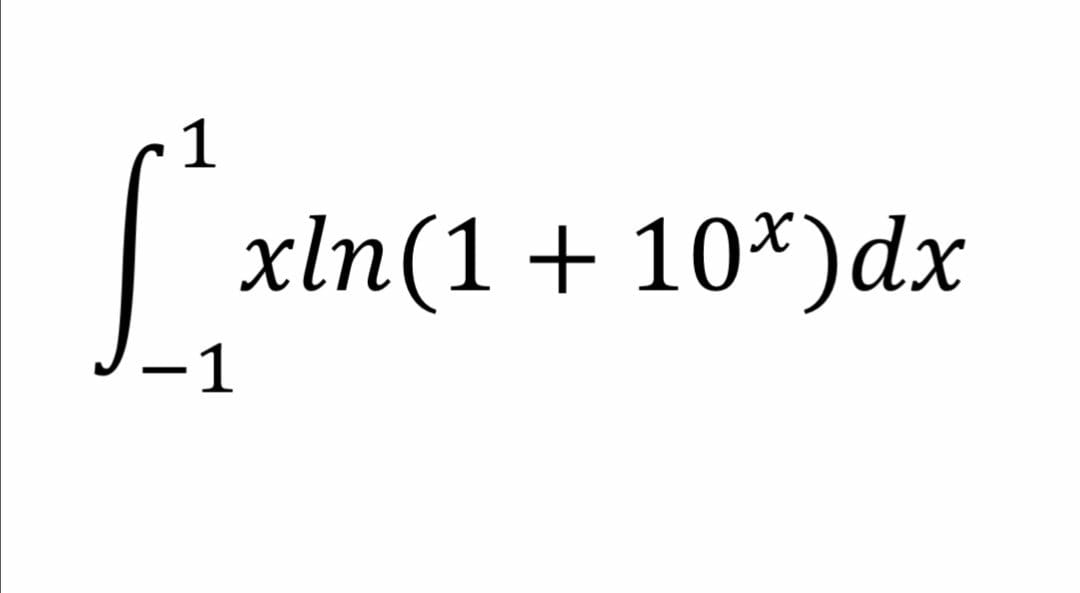
Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239

Contact: info@tinkutara.com