Question and Answers Forum

IntegrationQuestion and Answers: Page 223

Question Number 67937 Answers: 0 Comments: 1

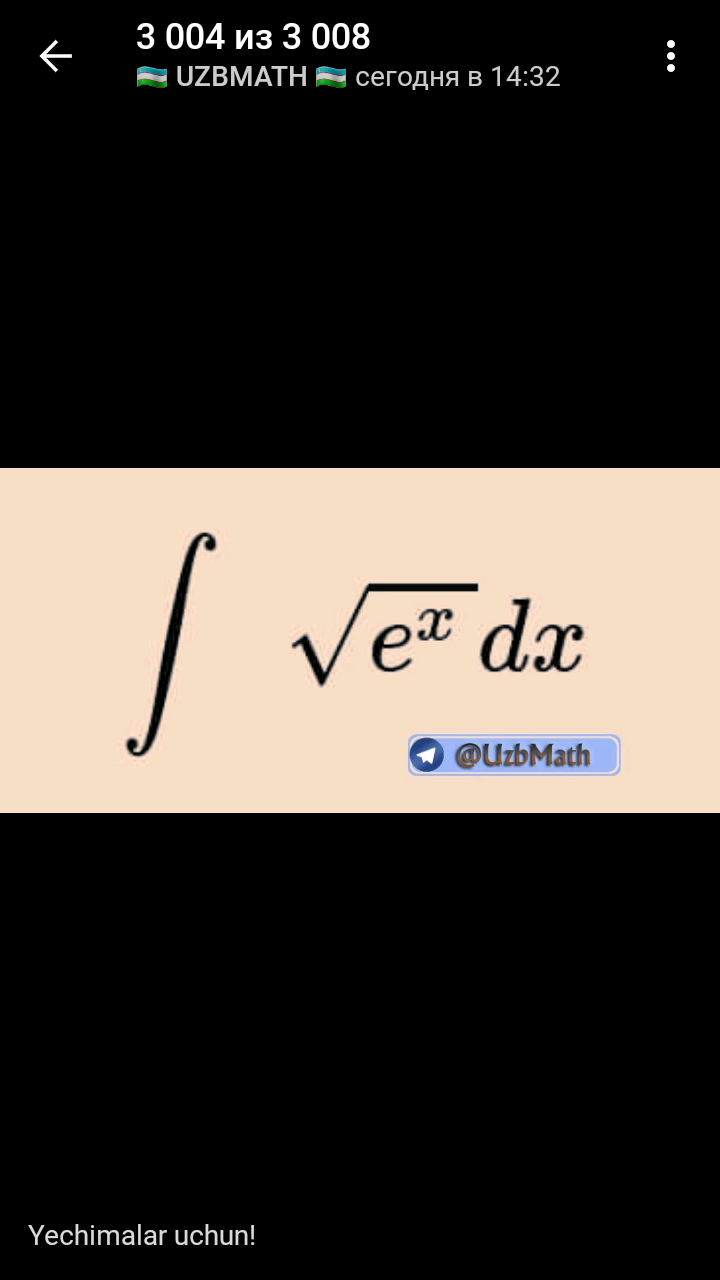
Question Number 67932 Answers: 1 Comments: 4

let A(θ) = ∫_0 ^∞ (dx/((x^2 +3)(x^4 −e^(iθ) ))) with 0<θ<(π/2) 1) calculate A(θ) interms of θ 2) determine also ∫_0 ^∞ (dx/((x^2 +3)(x^4 −e^(iθ) )^2 ))

$${let}\:{A}\left(\theta\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)}\:\:{with}\:\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}\left(\theta\right)\:{interms}\:{of}\:\theta \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{also}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)^{\mathrm{2}} } \\ $$

Question Number 67931 Answers: 0 Comments: 0

let A_n =∫_0 ^(π/4) x^n {1+cosx +cos(2x)}^2 dx find a relation of recurrence betwedn the A_n

$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{x}^{{n}} \left\{\mathrm{1}+{cosx}\:+{cos}\left(\mathrm{2}{x}\right)\right\}^{\mathrm{2}} {dx} \\ $$$${find}\:{a}\:{relation}\:{of}\:{recurrence}\:{betwedn}\:{the}\:{A}_{{n}} \\ $$

Question Number 67919 Answers: 0 Comments: 0

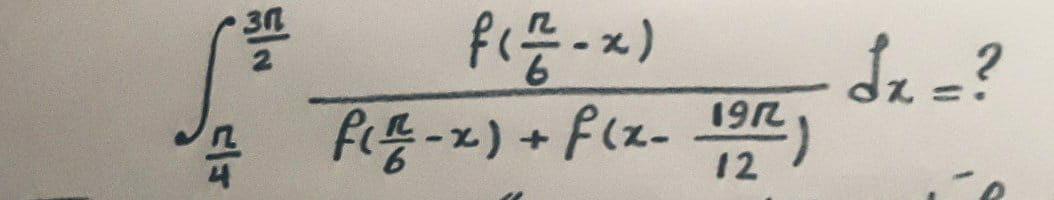
Question Number 67921 Answers: 0 Comments: 0

∫e^(y^2 /2) dy

$$\int{e}^{{y}^{\mathrm{2}} /\mathrm{2}} {dy} \\ $$

Question Number 67907 Answers: 1 Comments: 1

Question Number 67851 Answers: 0 Comments: 5

find ∫ (dx/(x^2 −z)) with z from C .

$${find}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{with}\:{z}\:{from}\:{C}\:. \\ $$

Question Number 67850 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) (dx/(x^2 −z)) with z from C

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{with}\:{z}\:{from}\:{C} \\ $$

Question Number 67835 Answers: 1 Comments: 0

∫_0 ^2 x(8−x^3 )^(1/3) dx

$$\int_{\mathrm{0}} ^{\mathrm{2}} {x}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$

Question Number 67823 Answers: 0 Comments: 0

∫_0 ^1 x^(lnx+e^(lnx/x) ) dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{lnx}+{e}^{{lnx}/{x}} } {dx} \\ $$

Question Number 67799 Answers: 1 Comments: 3

calculate ∫_0 ^∞ (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) with a>0 andb>0

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:−{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)}\:\:{with}\:{a}>\mathrm{0}\:{andb}>\mathrm{0} \\ $$

Question Number 67744 Answers: 0 Comments: 4

let f(x) =∫_0 ^∞ ((sin(t^2 ))/((x^2 +t^2 )^2 ))dt with x>0 1)determine a explicit form for f(x) 2) find also g(x) =∫_0 ^∞ ((sin(t^2 ))/((x^2 +t^2 )^3 ))dt 3) give f^((n)) (x) at form of integral and calculate f^((n)) (1). 4) find the valueof ∫_0 ^∞ ((sin(t^2 ))/((1+t^2 )^2 )) dt and ∫_0 ^∞ ((sin(t^2 ))/((1+t^2 )^3 ))dt

Question Number 67708 Answers: 1 Comments: 0

Question Number 67698 Answers: 0 Comments: 0

Question Number 67696 Answers: 0 Comments: 0

∫_0 ^1 (1−x)/(1+x)lnx dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)/\left(\mathrm{1}+{x}\right){lnx}\:{dx} \\ $$

Question Number 67674 Answers: 0 Comments: 3

let f(a) =∫_0 ^∞ (dx/((x^2 +1)(x^2 +a))) with a>0 1) determine a explicit form of f(a) 2) calculate g(a) =∫_0 ^∞ (dx/((x^2 +1)(x^2 +a)^2 )) 3)give f^((n)) (a) at form of integral 4)calculate ∫_0 ^∞ (dx/((x^2 +1)(x^2 +3)^2 )) and ∫_0 ^∞ (dx/((x^2 +1)^3 ))

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{a}\right)}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{g}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{a}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){give}\:{f}^{\left({n}\right)} \left({a}\right)\:{at}\:{form}\:{of}\:{integral} \\ $$$$\left.\mathrm{4}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Question Number 67673 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +x+1)))

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)} \\ $$

Question Number 67628 Answers: 0 Comments: 0

∫x^n lnx/n^(x ) dx

$$\int{x}^{{n}} {lnx}/{n}^{{x}\:} \:{dx} \\ $$

Question Number 67618 Answers: 1 Comments: 0

find the area abovnded r=cos2θ

$${find}\:{the}\:{area}\:{abovnded}\:{r}={cos}\mathrm{2}\theta \\ $$

Question Number 67617 Answers: 0 Comments: 2

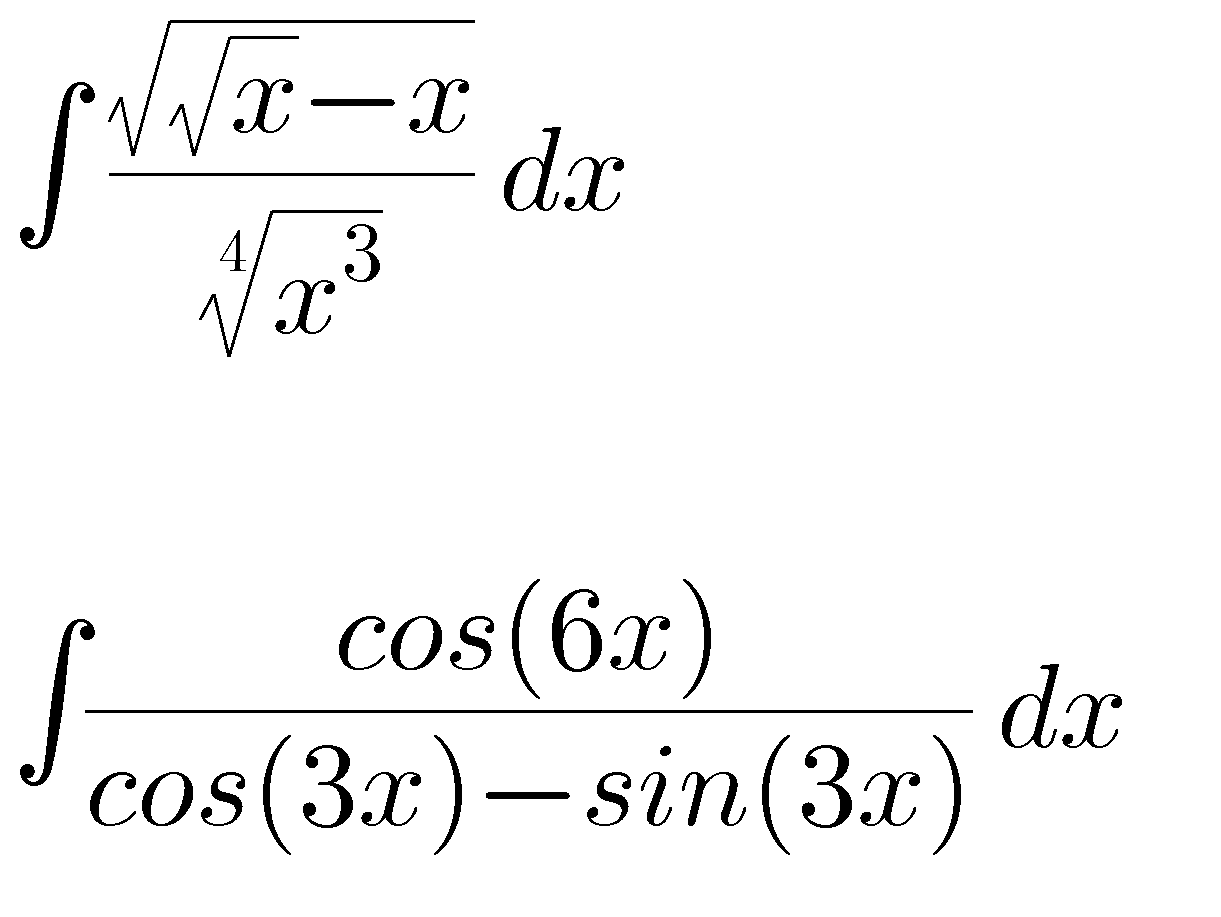
Question Number 67572 Answers: 0 Comments: 1

∫_(−(π/2)) ^(π/2) {sin∣x∣+cos∣x∣} dx

$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left\{{sin}\mid{x}\mid+{cos}\mid{x}\mid\right\}\:{dx} \\ $$

Question Number 67542 Answers: 0 Comments: 4

let f(a) =∫_(−∞) ^(+∞) (dx/((x^2 +1)(a +e^(ix) ))) with a>0 1)find a explicit form of f(a) 2) determine also g(a)=∫_(−∞) ^(+∞) (dx/((x^2 +1)(a+e^(ix) )^2 )) 3)let I =Re(∫_(−∞) ^(+∞) (dx/((x^2 +1)(2+e^(ix) )))) and J=Im(∫_(−∞) ^(+∞) (dx/((x^2 +1)(2+e^x )))) determine I and J and its values.

$${let}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({a}\:+{e}^{{ix}} \right)}\:\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{also}\:{g}\left({a}\right)=\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({a}+{e}^{{ix}} \right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){let}\:{I}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}+{e}^{{ix}} \right)}\right)\:{and}\:{J}={Im}\left(\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}+{e}^{{x}} \right)}\right) \\ $$$$\:{determine}\:{I}\:{and}\:{J}\:\:{and}\:\:{its}\:{values}. \\ $$

Question Number 67539 Answers: 0 Comments: 3

calculate ∫_0 ^∞ (du/(∣u+z∣^2 )) if z =r e^(iθ) and −π<θ<π

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mid{u}+{z}\mid^{\mathrm{2}} }\:\:{if}\:{z}\:={r}\:{e}^{{i}\theta} \:\:\:{and}\:−\pi<\theta<\pi \\ $$

Question Number 67531 Answers: 0 Comments: 1

prove that cos(πz) =Π_(n=1) ^∞ (1−(z^2 /(((1/2)+n)^2 )))

$${prove}\:{that}\:{cos}\left(\pi{z}\right)\:=\prod_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\left(\frac{\mathrm{1}}{\mathrm{2}}+{n}\right)^{\mathrm{2}} }\right) \\ $$

Question Number 67530 Answers: 0 Comments: 2

calculate ∫_0 ^∞ (x^(n−3) /(1+x^(2n) ))dx with n≥3

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{n}−\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}{n}} }{dx}\:\:{with}\:{n}\geqslant\mathrm{3} \\ $$

Question Number 67528 Answers: 0 Comments: 3

calculate ∫_(−∞) ^(+∞) ((1+x^3 )/(1+x^6 ))dx

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx} \\ $$

Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227

Contact: info@tinkutara.com