Question and Answers Forum

IntegrationQuestion and Answers: Page 213

Question Number 75177 Answers: 2 Comments: 2

Question Number 75141 Answers: 1 Comments: 2

Question Number 75102 Answers: 0 Comments: 0

show by integration that the centroid of a semi−circular lamina of radius a from the centre is ((4a)/(3π)).

$$\mathrm{show}\:\mathrm{by}\:\mathrm{integration}\:\mathrm{that}\:\mathrm{the}\:\mathrm{centroid} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{semi}−\mathrm{circular}\:\mathrm{lamina}\:\mathrm{of}\:\mathrm{radius}\:{a}\: \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{is}\:\:\:\frac{\mathrm{4}{a}}{\mathrm{3}\pi}. \\ $$

Question Number 75098 Answers: 1 Comments: 0

the function f is defined by f(x) = (2/(x^2 −1)) a) Express f into partial fraction b.show that ∫_3 ^5 f(x) dx = ln((4/3))

$$\mathrm{the}\:\mathrm{function}\:\mathrm{f}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{by}\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\left.{a}\right)\:\mathrm{Express}\:\mathrm{f}\:\mathrm{into}\:\mathrm{partial}\:\mathrm{fraction} \\ $$$$\mathrm{b}.\mathrm{show}\:\mathrm{that}\:\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right)\:{dx}\:=\:{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$

Question Number 75093 Answers: 1 Comments: 1

∫cos^3 xsin^3 xdx

$$\int{cos}^{\mathrm{3}} {xsin}^{\mathrm{3}} {xdx} \\ $$

Question Number 75082 Answers: 1 Comments: 0

find ∫_0 ^π e^(cosx) sinx dx

$${find} \\ $$$$\int_{\mathrm{0}} ^{\pi} {e}^{{cosx}} {sinx}\:{dx} \\ $$

Question Number 75081 Answers: 1 Comments: 0

Evaluate ∫_1 ^(3 ) (x^2 /(1+x)) dx

$${Evaluate}\: \\ $$$$\:\int_{\mathrm{1}} ^{\mathrm{3}\:} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}\:{dx} \\ $$

Question Number 75034 Answers: 3 Comments: 0

Question Number 75027 Answers: 1 Comments: 1

Question Number 74997 Answers: 1 Comments: 1

Question Number 74995 Answers: 1 Comments: 1

find ∫_0 ^(π/2) Log cosx dx

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{Log}\:\mathrm{cos}{x}\:{dx} \\ $$

Question Number 74891 Answers: 0 Comments: 4

Q. How will you define integrating constant C ? In how many ways can you define C ?

$$\mathrm{Q}.\:\mathrm{How}\:\mathrm{will}\:\mathrm{you}\:\mathrm{define}\:\mathrm{integrating}\: \\ $$$$\mathrm{constant}\:\mathrm{C}\:?\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{you} \\ $$$$\mathrm{define}\:\mathrm{C}\:? \\ $$$$ \\ $$

Question Number 74890 Answers: 1 Comments: 1

find ∫ (x+3)(√((x−1)(2−x)))dx

$${find}\:\int\:\:\:\left({x}+\mathrm{3}\right)\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}{dx} \\ $$

Question Number 74889 Answers: 1 Comments: 1

find ∫_(−(1/2)) ^(+∞) e^(−x) (√(2x+1))dx

$${find}\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{+\infty} \:\:{e}^{−{x}} \sqrt{\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$

Question Number 74888 Answers: 1 Comments: 3

calculate f(α)=∫(√(x^2 −x+α))dx (α real)

$${calculate}\:{f}\left(\alpha\right)=\int\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}{dx}\:\:\left(\alpha\:{real}\right) \\ $$

Question Number 74886 Answers: 0 Comments: 1

calculate ∫ ((x+1)/((x^3 +x−2)^2 ))dx

$${calculate}\:\int\:\:\frac{{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} +{x}−\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 74861 Answers: 1 Comments: 0

Question Number 74799 Answers: 1 Comments: 0

prove that 0≤∫_0 ^∞ ((t^2 e^(−nt) )/(e^t −1))dt ≤(1/n^2 ) for n integr not 0

$${prove}\:{that}\:\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\mathrm{2}} \:{e}^{−{nt}} }{{e}^{{t}} −\mathrm{1}}{dt}\:\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:{for}\:{n}\:{integr}\:{not}\:\mathrm{0} \\ $$

Question Number 74798 Answers: 0 Comments: 0

calculate ∫_0 ^π ln(1−2xcosθ +x^2 )dθ with ∣x∣<1

$${calculate}\:\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}−\mathrm{2}{xcos}\theta\:+{x}^{\mathrm{2}} \right){d}\theta\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$

Question Number 74796 Answers: 0 Comments: 0

let U_n =(−1)^n {arcsin((1/n))−(1/n)}^(1/3) study the convergence of Σ U_n

$${let}\:{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left\{{arcsin}\left(\frac{\mathrm{1}}{{n}}\right)−\frac{\mathrm{1}}{{n}}\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${study}\:{the}\:{convergence}\:{of}\:\Sigma\:{U}_{{n}} \\ $$

Question Number 74793 Answers: 1 Comments: 1

prove the convergence of ∫_0 ^1 ((ln(1+(√x)))/(√x))dx

$${prove}\:{the}\:{convergence}\:{of}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\sqrt{{x}}\right)}{\sqrt{{x}}}{dx} \\ $$

Question Number 74720 Answers: 2 Comments: 5

Question Number 74944 Answers: 0 Comments: 0

∫(e^(−cos(2x)) /(sin^2 (x))) dx

$$\int\frac{{e}^{−{cos}\left(\mathrm{2}{x}\right)} }{{sin}^{\mathrm{2}} \left({x}\right)}\:{dx} \\ $$

Question Number 74621 Answers: 1 Comments: 1

Question Number 74620 Answers: 1 Comments: 0

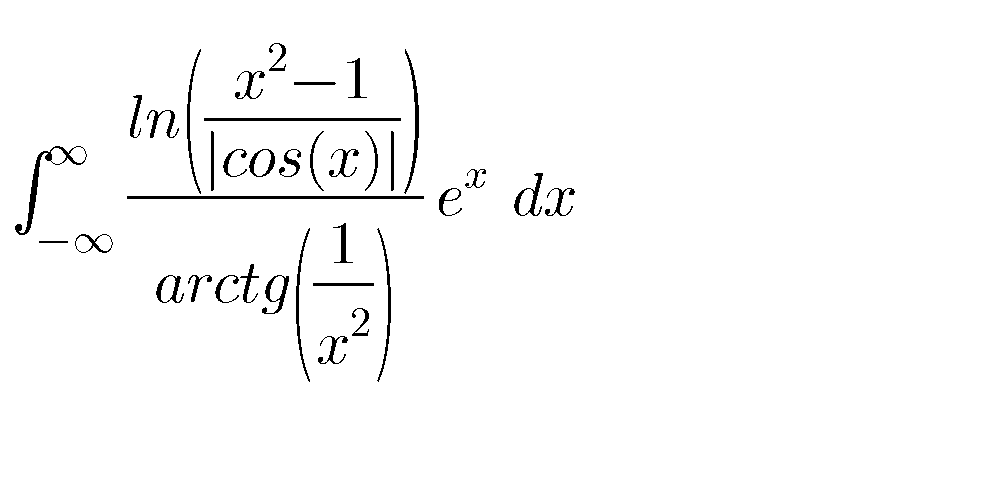
Question Number 74514 Answers: 1 Comments: 1

calculate ∫_0 ^(2π) (((x−sinθ)dθ)/((x^2 −2x sinθ +1)^2 ))

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{\left({x}−{sin}\theta\right){d}\theta}{\left({x}^{\mathrm{2}} −\mathrm{2}{x}\:{sin}\theta\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Pg 208 Pg 209 Pg 210 Pg 211 Pg 212 Pg 213 Pg 214 Pg 215 Pg 216 Pg 217

Contact: [email protected]