Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 204

Question Number 80846 Answers: 1 Comments: 4

Question Number 80788 Answers: 0 Comments: 0

Question Number 80770 Answers: 1 Comments: 1

∫x^2 +3x dx=..

$$\int\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\:\mathrm{dx}=.. \\ $$

Question Number 80764 Answers: 1 Comments: 0

show that ∫_0 ^∞ x arctanh(e^(−αx) )dx=((7ζ(3))/(8α^2 ))

$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}\:{arctanh}\left({e}^{−\alpha{x}} \right){dx}=\frac{\mathrm{7}\zeta\left(\mathrm{3}\right)}{\mathrm{8}\alpha^{\mathrm{2}} } \\ $$

Question Number 80752 Answers: 1 Comments: 1

Question Number 80612 Answers: 0 Comments: 3

Ψ(x)=∫_1 ^x (1/(√(1−e^t ))) dt ∀x∈R prove that Ψ(x)=2ln(((1−(√(1−e^x )))/(1−(√(1−e)))))−x+1

$$\:\Psi\left({x}\right)=\int_{\mathrm{1}} ^{{x}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−{e}^{{t}} }}\:{dt}\:\:\:\:\:\forall{x}\in\mathbb{R} \\ $$$${prove}\:{that} \\ $$$$\Psi\left({x}\right)=\mathrm{2}{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{1}−{e}^{{x}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{e}}}\right)−{x}+\mathrm{1} \\ $$

Question Number 80485 Answers: 0 Comments: 1

what is the king rule?

$${what}\:{is}\:{the}\:{king}\:\:{rule}? \\ $$

Question Number 80452 Answers: 0 Comments: 1

find ∫_(−∞) ^(+∞) ((cos(2x^2 +1))/(x^4 −x^2 +3))dx

$${find}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$

Question Number 80451 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((cos(πx))/((x^2 +3)^2 ))dx

$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left(\pi{x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 80432 Answers: 0 Comments: 7

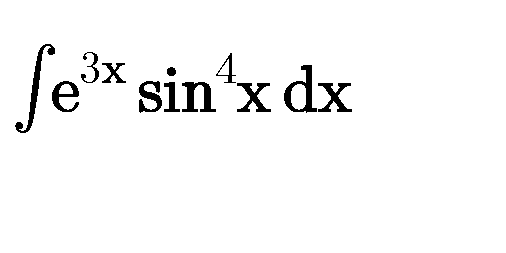
Question Number 80416 Answers: 1 Comments: 0

∫_0 ^(π/2) ((xcos x)/((1+sin x)^2 )) dx ?

$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{x}\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:{dx}\:? \\ $$

Question Number 80397 Answers: 0 Comments: 3

show that ∫_0 ^(π/2) ∫_0 ^∞ (1/((x^π )^(1/y) +1)) dx dy =2c whrre c denote tha catalan^, s constant

$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\sqrt[{{y}}]{{x}^{\pi} }\:+\mathrm{1}}\:{dx}\:{dy}\:=\mathrm{2}{c}\: \\ $$$${whrre}\:{c}\:{denote}\:{tha}\:{catalan}^{,} {s}\:{constant} \\ $$

Question Number 80369 Answers: 0 Comments: 1

Question Number 80334 Answers: 0 Comments: 1

let f∈L^1 (R) let u_n = ∫_a ^b f(t)sin(nt)dt , v_n =∫_a ^b ((f(t))/t)sin(nt) 1)Prove that lim_(n→∞) u_n =0 2)Deduce in term of a,b,f(0) the value of lim_(n→∞) v_n

$$\:{let}\:\:\:{f}\in{L}^{\mathrm{1}} \left(\mathbb{R}\right)\:\:\: \\ $$$${let}\:\:{u}_{{n}} =\:\int_{{a}} ^{{b}} {f}\left({t}\right){sin}\left({nt}\right){dt}\:,\:{v}_{{n}} =\int_{{a}} ^{{b}} \frac{{f}\left({t}\right)}{{t}}{sin}\left({nt}\right)\: \\ $$$$\left.\mathrm{1}\right){Prove}\:{that}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{u}_{{n}} =\mathrm{0} \\ $$$$\left.\mathrm{2}\right){Deduce}\:\:{in}\:{term}\:{of}\:{a},{b},{f}\left(\mathrm{0}\right)\:{the}\:{value}\:{of}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{v}_{{n}} \:\: \\ $$

Question Number 80332 Answers: 0 Comments: 1

let α ∈R and a_n =Σ_(k=1) ^n ((sin(kα))/(n+k)) Find lim_(n→∞) a_n

$$\:\:{let}\:\alpha\:\in\mathbb{R}\:\:{and}\:\:\:\:{a}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{sin}\left({k}\alpha\right)}{{n}+{k}} \\ $$$${Find}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:{a}_{{n}} \: \\ $$

Question Number 80312 Answers: 1 Comments: 17

Question Number 80300 Answers: 0 Comments: 4

Question Number 80227 Answers: 0 Comments: 5

how to prove ∫_0 ^1 x^n (1−x)^(m ) dx = ((m! ×n!)/((m+n)!)) via Gamma function

$${how}\:{to}\:{prove} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{{n}} \:\left(\mathrm{1}−{x}\right)^{{m}\:} \:{dx}\:=\:\frac{{m}!\:×{n}!}{\left({m}+{n}\right)!} \\ $$$${via}\:{Gamma}\:{function} \\ $$

Question Number 80052 Answers: 0 Comments: 0

∫ e^(sin 2x) .cos x dx =

$$\int\:\mathrm{e}^{\mathrm{sin}\:\mathrm{2x}} .\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}\:= \\ $$$$ \\ $$

Question Number 79929 Answers: 0 Comments: 0

∫e^(√(sin x)) dx=?

$$\int{e}^{\sqrt{\mathrm{sin}\:{x}}} {dx}=? \\ $$

Question Number 79913 Answers: 0 Comments: 1

Convergence of I=∫_0 ^( ∞) (e^t /(e^(−t) +e^(2t) ∣sint∣))dt

$$\:{Convergence}\:\:{of}\:\:{I}=\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{{t}} }{{e}^{−{t}} +{e}^{\mathrm{2}{t}} \mid{sint}\mid}{dt} \\ $$

Question Number 79903 Answers: 1 Comments: 11

Question Number 79869 Answers: 0 Comments: 1

For witch value of α the integral I=∫_0 ^∞ ((1/(√(1+2x^2 )))−(α/(1+x)))dx converge; and in this case calculate α

$${For}\:\:{witch}\:\:{value}\:\:{of}\:\:\alpha\:\:{the}\:\:{integral} \\ $$$$\:\:{I}=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\right){dx}\:\:{converge}; \\ $$$$\:\:{and}\:\:{in}\:\:{this}\:\:{case}\:\:{calculate}\:\:\alpha \\ $$

Question Number 79837 Answers: 1 Comments: 10

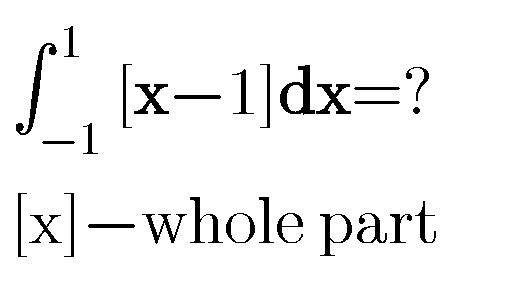
Question Number 79825 Answers: 0 Comments: 4

∫_( 0) ^( 1) (√(x^3 + 1)) dx

$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\sqrt{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{1}}\:\:\mathrm{dx} \\ $$

Question Number 79824 Answers: 2 Comments: 7

Pg 199 Pg 200 Pg 201 Pg 202 Pg 203 Pg 204 Pg 205 Pg 206 Pg 207 Pg 208

Contact: info@tinkutara.com