Question and Answers Forum

show that ∫(1/([x(x−1)(x−2)(x−3)...(x−m)]^2 ))dx= =(1/((m!)^2 ))Σ_(n=0) ^m ( ((m),(n) )^2 /(n−x))+(2/((m!)^2 ))ln∣Π_(n=0) ^m (x−n)^( ((m),(n) )^2 (H_(m−n) −H_n )) ∣+c

$${show}\:{that} \\ $$$$\int\frac{\mathrm{1}}{\left[{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)...\left({x}−{m}\right)\right]^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{1}}{\left({m}!\right)^{\mathrm{2}} }\underset{{n}=\mathrm{0}} {\overset{{m}} {\sum}}\frac{\begin{pmatrix}{{m}}\\{{n}}\end{pmatrix}^{\mathrm{2}} }{{n}−{x}}+\frac{\mathrm{2}}{\left({m}!\right)^{\mathrm{2}} }{ln}\mid\underset{{n}=\mathrm{0}} {\overset{{m}} {\prod}}\left({x}−{n}\right)^{\begin{pmatrix}{{m}}\\{{n}}\end{pmatrix}^{\mathrm{2}} \left({H}_{{m}−{n}} −{H}_{{n}} \right)} \mid+{c} \\ $$

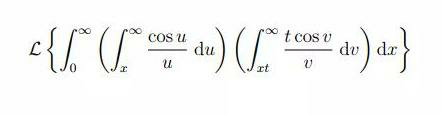
Question Number 85641 Answers: 0 Comments: 2

calculate A_λ =∫_3 ^∞ (dx/((x+λ)^3 (x−2)^4 )) (λ>0)

$${calculate}\:{A}_{\lambda} =\int_{\mathrm{3}} ^{\infty} \:\:\frac{{dx}}{\left({x}+\lambda\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{4}} }\:\:\:\left(\lambda>\mathrm{0}\right) \\ $$

Question Number 85637 Answers: 1 Comments: 2

∫ (dx/(x+(√(x^2 +1))))

$$\int\:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\: \\ $$

Question Number 85603 Answers: 0 Comments: 0

prove the relation ∫_0 ^1 ((li_5 ((x)^(1/5) ))/(x)^(1/5) )dx=(5/4)(((25)/(3072))−((ζ(2))/2^6 )+((ζ(3))/2^4 )−((ζ(4))/2^2 )+ζ(5))

$${prove}\:{the}\:{relation} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{li}_{\mathrm{5}} \left(\sqrt[{\mathrm{5}}]{{x}}\right)}{\sqrt[{\mathrm{5}}]{{x}}}{dx}=\frac{\mathrm{5}}{\mathrm{4}}\left(\frac{\mathrm{25}}{\mathrm{3072}}−\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}^{\mathrm{6}} }+\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}^{\mathrm{4}} }−\frac{\zeta\left(\mathrm{4}\right)}{\mathrm{2}^{\mathrm{2}} }+\zeta\left(\mathrm{5}\right)\right) \\ $$

Question Number 85592 Answers: 1 Comments: 0

∫(((u+1)^2 )/(u^3 +u))du

$$\int\frac{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{u}^{\mathrm{3}} +\mathrm{u}}\mathrm{du} \\ $$

Question Number 85591 Answers: 1 Comments: 0

∫((1+4u)/(−4u^2 +2u+2))du

$$\int\frac{\mathrm{1}+\mathrm{4u}}{−\mathrm{4u}^{\mathrm{2}} +\mathrm{2u}+\mathrm{2}}\mathrm{du} \\ $$$$ \\ $$

Question Number 85590 Answers: 0 Comments: 0

∫((1+4u)/(−4u^2 +2u+2))du

$$\int\frac{\mathrm{1}+\mathrm{4u}}{−\mathrm{4u}^{\mathrm{2}} +\mathrm{2u}+\mathrm{2}}\mathrm{du} \\ $$$$ \\ $$

Question Number 85601 Answers: 0 Comments: 2

∫((4u)/(4u^2 −4u+1))du

$$\int\frac{\mathrm{4u}}{\mathrm{4u}^{\mathrm{2}} −\mathrm{4u}+\mathrm{1}}\mathrm{du} \\ $$

Question Number 85600 Answers: 1 Comments: 3

∫(x^2 /(√(1+x^2 ))) dx

$$\int\frac{{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$

Question Number 85596 Answers: 1 Comments: 1

∫(((√(x+1))−1)/((√(x−1))+1)) dx

$$\int\frac{\sqrt{{x}+\mathrm{1}}−\mathrm{1}}{\sqrt{{x}−\mathrm{1}}+\mathrm{1}}\:{dx} \\ $$

Question Number 85568 Answers: 4 Comments: 2

∫ _0 ^(2π) (dx/((√2)−cos x))

$$\int\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\:}}\:\frac{\mathrm{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\mathrm{x}} \\ $$

Question Number 85551 Answers: 0 Comments: 1

∫ (dx/(x^2 (x^4 +1)^(3/4) ))

$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$

Pg 189 Pg 190 Pg 191 Pg 192 Pg 193 Pg 194 Pg 195 Pg 196 Pg 197 Pg 198

Contact: info@tinkutara.com