
IntegrationQuestion and Answers: Page 187
Question Number 88603 Answers: 1 Comments: 0

Question Number 88586 Answers: 1 Comments: 0
$$\int\frac{\sqrt{{cos}\left(\mathrm{2}{x}\right)+\mathrm{3}}}{{cos}\left({x}\right)}{dx} \\ $$
Question Number 88569 Answers: 1 Comments: 1

Question Number 88555 Answers: 1 Comments: 0
Question Number 88547 Answers: 1 Comments: 0
Question Number 88490 Answers: 0 Comments: 4
$$\int_{\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{4}} }{\mathrm{4}^{{x}} }{dx}=? \\ $$
Question Number 88462 Answers: 0 Comments: 3

Question Number 88438 Answers: 2 Comments: 0
$$\int\frac{{x}^{\mathrm{5}} +\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}}{dx} \\ $$
Question Number 88429 Answers: 0 Comments: 0
Question Number 88422 Answers: 0 Comments: 1
Question Number 88415 Answers: 0 Comments: 2
Question Number 88414 Answers: 0 Comments: 2
Question Number 88413 Answers: 0 Comments: 3
$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$ \\ $$
Question Number 88388 Answers: 1 Comments: 0
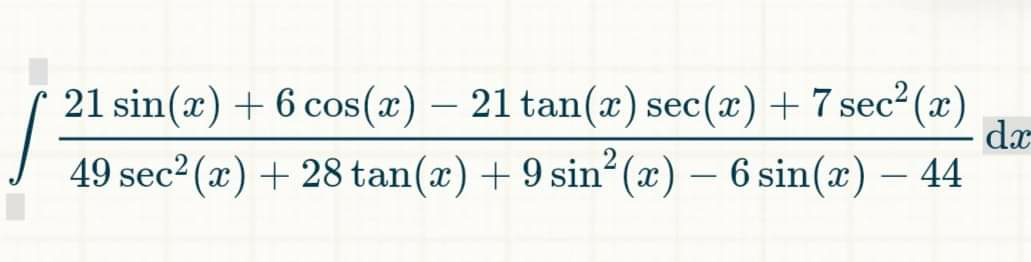
Question Number 88357 Answers: 0 Comments: 1
Question Number 88307 Answers: 1 Comments: 0
Question Number 88286 Answers: 0 Comments: 1

Question Number 88253 Answers: 0 Comments: 0
$$\int\:\frac{\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:{dx}}{{x}+\mathrm{1}}\: \\ $$
Question Number 88206 Answers: 1 Comments: 0
Question Number 88197 Answers: 0 Comments: 0
Question Number 88196 Answers: 0 Comments: 0

Question Number 88194 Answers: 0 Comments: 4
Question Number 88181 Answers: 0 Comments: 1

Question Number 88177 Answers: 1 Comments: 0
Question Number 88170 Answers: 0 Comments: 2
Question Number 88153 Answers: 0 Comments: 1
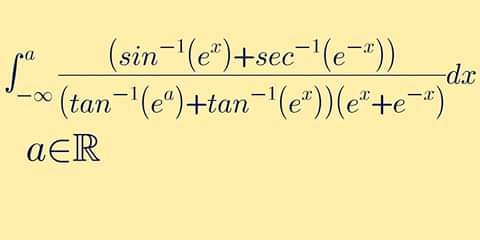
Pg 182 Pg 183 Pg 184 Pg 185 Pg 186 Pg 187 Pg 188 Pg 189 Pg 190 Pg 191
