Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 158

Question Number 105386 Answers: 2 Comments: 0

∫ (x^3 /(√((a^2 +x^2 )^3 ))) dx

$$\int\:\frac{{x}^{\mathrm{3}} }{\sqrt{\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:{dx}\: \\ $$

Question Number 105353 Answers: 0 Comments: 0

solve y^(′′ ) +2y^′ −y =x^n e^(−x) n integr natural

$${solve}\:{y}^{''\:} +\mathrm{2}{y}^{'} −{y}\:={x}^{{n}} \:{e}^{−{x}} \\ $$$${n}\:{integr}\:{natural} \\ $$

Question Number 105233 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((ch(cosx)−cos(chx))/(x^2 +3))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ch}\left(\mathrm{cosx}\right)−\mathrm{cos}\left(\mathrm{chx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}}\mathrm{dx} \\ $$

Question Number 105232 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((cos(2x^2 ))/((4x^2 +9)^3 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{2x}^{\mathrm{2}} \right)}{\left(\mathrm{4x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$

Question Number 105231 Answers: 1 Comments: 0

calculate ∫_0 ^(+∞) ((2x^2 −1)/((x^2 +x+1)^2 (x^2 −x+1)^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 105230 Answers: 2 Comments: 0

calculate ∫_1 ^(+∞) (dx/((x^2 +1)^2 (x^2 +4)^2 ))

$$\mathrm{calculate}\:\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} } \\ $$

Question Number 142176 Answers: 1 Comments: 0

∫ e^(ax) sin bx dx = ?

$$\int\:{e}^{{ax}} \:{sin}\:{bx}\:{dx}\:=\:? \\ $$

Question Number 104928 Answers: 0 Comments: 5

∫ (e^x −(2x+3)^4 )^3 dx

$$\int\:\left({e}^{{x}} −\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} \right)^{\mathrm{3}} \:{dx} \\ $$

Question Number 104910 Answers: 0 Comments: 0

∫_0 ^1 (1/(√(1+x^3 )))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}{dx} \\ $$

Question Number 104890 Answers: 1 Comments: 0

lim_(n→∞) (1/n)Σ_(k=1) ^n [1+(k^3 /n^3 )]^(−(1/2))

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\mathrm{1}+\frac{\mathrm{k}^{\mathrm{3}} }{\mathrm{n}^{\mathrm{3}} }\right]^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Question Number 104980 Answers: 1 Comments: 3

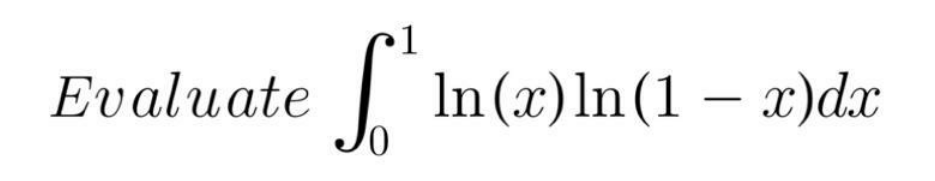
Question Number 104871 Answers: 2 Comments: 0

Question Number 104826 Answers: 1 Comments: 1

∫3^(x+2) ∙lnsin3^x dx=???

$$\int\mathrm{3}^{{x}+\mathrm{2}} \centerdot{lnsin}\mathrm{3}^{{x}} {dx}=??? \\ $$

Question Number 104773 Answers: 1 Comments: 0

let A_n =∫∫_([0,n[^2 ) (e^(−x^2 −y^2 ) /(√(x^2 +y^2 )))dxdy 1) calculste A_n interm of n 2) find lim_(n→+∞) A_n

$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int\int_{\left[\mathrm{0},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\:\:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } }{\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }}\mathrm{dxdy} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculste}\:\mathrm{A}_{\mathrm{n}} \:\mathrm{interm}\:\mathrm{of}\:\mathrm{n} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} \\ $$

Question Number 104774 Answers: 1 Comments: 0

let B_n = ∫∫_([0,n[^2 ) ((arctan(x^2 +3y^2 ))/(√(x^2 +3y^2 )))dxdy calculate lim_(n→+∞) (B_n /n)

$$\mathrm{let}\:\mathrm{B}_{\mathrm{n}} =\:\int\int_{\left[\mathrm{0},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3y}^{\mathrm{2}} \right)}{\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3y}^{\mathrm{2}} }}\mathrm{dxdy} \\ $$$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{B}_{\mathrm{n}} }{\mathrm{n}} \\ $$

Question Number 104732 Answers: 0 Comments: 0

∫_0 ^1 log(tanθ)dθ

$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({tan}\theta\right){d}\theta \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 104718 Answers: 2 Comments: 0

∫tan^(−1) (((a(√x)+b)/c))dx

$$\int{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right){dx}\: \\ $$

Question Number 104645 Answers: 1 Comments: 1

Question Number 104644 Answers: 1 Comments: 0

∫_0 ^1 ((log(1−x+x^2 −x^3 +x^4 )dx)/x) = −(π^2 /(15))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right){dx}}{{x}}\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{15}} \\ $$

Question Number 104609 Answers: 1 Comments: 0

prove: ∫_0 ^1 ((x^4 (1−x)^4 )/(1+x^2 ))dx=((22)/7)−π

$${prove}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{22}}{\mathrm{7}}−\pi \\ $$

Question Number 104602 Answers: 0 Comments: 0

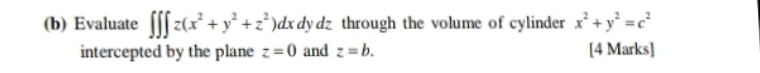
Question Number 104523 Answers: 0 Comments: 0

∫((xdx)/((x^3 +x+1)^2 ))

$$\int\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 104505 Answers: 1 Comments: 0

calculate ∫_0 ^∞ (dx/((x+1)^2 (x+2)^2 (x+3)^2 ))

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$

Question Number 104459 Answers: 1 Comments: 1

∫ (dx/(√(Acos x+B)))

$$\int\:\frac{{dx}}{\sqrt{{A}\mathrm{cos}\:{x}+{B}}} \\ $$

Question Number 104421 Answers: 0 Comments: 0

calculate ∫_(−∞) ^(+∞) ((ch(arctan(2x)))/(x^2 +x+1))dx

$$\mathrm{calculate}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{ch}\left(\mathrm{arctan}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$

Question Number 104388 Answers: 1 Comments: 0

∫(dx/(x^2 ((x^3 −1))^(1/3) ))

$$\int\frac{\mathrm{d}{x}}{{x}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{1}}} \\ $$

Pg 153 Pg 154 Pg 155 Pg 156 Pg 157 Pg 158 Pg 159 Pg 160 Pg 161 Pg 162

Contact: info@tinkutara.com