
IntegrationQuestion and Answers: Page 151
Question Number 110215 Answers: 1 Comments: 1
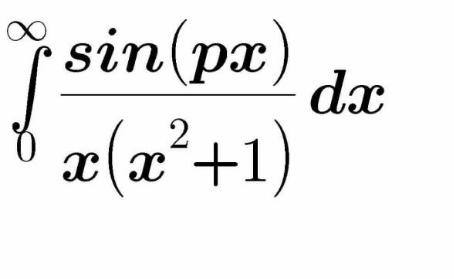
Question Number 110203 Answers: 1 Comments: 0

Question Number 110143 Answers: 2 Comments: 0
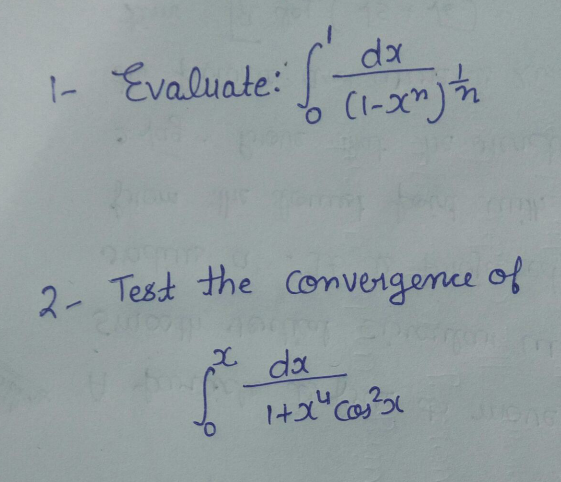
Question Number 110027 Answers: 2 Comments: 0

Question Number 109989 Answers: 1 Comments: 1

Question Number 109988 Answers: 0 Comments: 0
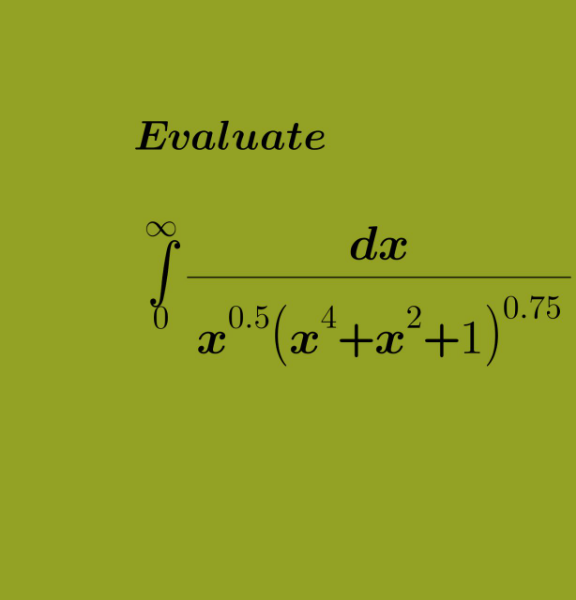
Question Number 109949 Answers: 1 Comments: 0

Question Number 109891 Answers: 1 Comments: 0
Question Number 109884 Answers: 1 Comments: 1

Question Number 109872 Answers: 2 Comments: 1
Question Number 109849 Answers: 0 Comments: 0

Question Number 109839 Answers: 4 Comments: 1
Question Number 109838 Answers: 1 Comments: 0
Question Number 109801 Answers: 0 Comments: 2
Question Number 109794 Answers: 0 Comments: 0
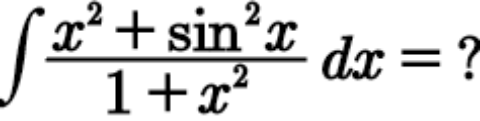
Question Number 109709 Answers: 2 Comments: 0
Question Number 109658 Answers: 1 Comments: 0

Question Number 109848 Answers: 0 Comments: 0

Question Number 109642 Answers: 1 Comments: 0
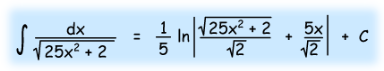
Question Number 109616 Answers: 1 Comments: 1
Question Number 109546 Answers: 1 Comments: 2
Question Number 109506 Answers: 0 Comments: 0

Question Number 109509 Answers: 4 Comments: 0
Question Number 109472 Answers: 4 Comments: 0
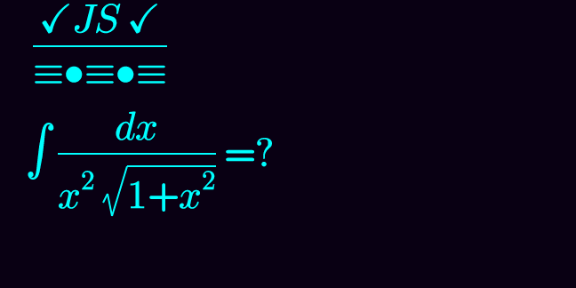
Question Number 109459 Answers: 0 Comments: 0

Question Number 109457 Answers: 3 Comments: 0

Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153 Pg 154 Pg 155
