
IntegrationQuestion and Answers: Page 149
Question Number 111189 Answers: 4 Comments: 0
Question Number 111174 Answers: 0 Comments: 0
Question Number 111109 Answers: 0 Comments: 0

Question Number 111104 Answers: 2 Comments: 2

Question Number 111048 Answers: 0 Comments: 0
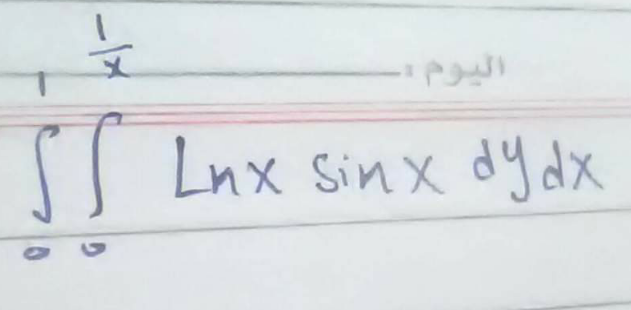
Question Number 111083 Answers: 2 Comments: 0
Question Number 111082 Answers: 1 Comments: 1
Question Number 111027 Answers: 0 Comments: 0
Question Number 111025 Answers: 1 Comments: 0
Question Number 111024 Answers: 1 Comments: 0
Question Number 111010 Answers: 1 Comments: 0
Question Number 111017 Answers: 2 Comments: 0
Question Number 110875 Answers: 4 Comments: 0
Question Number 110800 Answers: 0 Comments: 0
$$\int\frac{{sin}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Question Number 110772 Answers: 0 Comments: 0
Question Number 110749 Answers: 1 Comments: 0
Question Number 118674 Answers: 1 Comments: 0
Question Number 110551 Answers: 2 Comments: 0
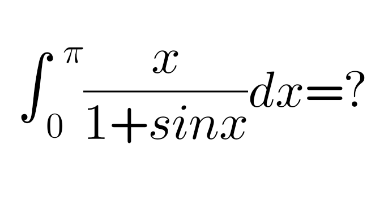
Question Number 110549 Answers: 2 Comments: 1
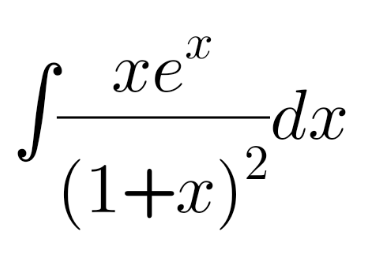
Question Number 110543 Answers: 1 Comments: 0

Question Number 110888 Answers: 3 Comments: 0
Question Number 110451 Answers: 1 Comments: 0
Question Number 110450 Answers: 1 Comments: 0
Question Number 110448 Answers: 1 Comments: 0
Question Number 110447 Answers: 1 Comments: 0
Question Number 110301 Answers: 0 Comments: 1

Pg 144 Pg 145 Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153
