Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 147

Question Number 113421 Answers: 0 Comments: 2

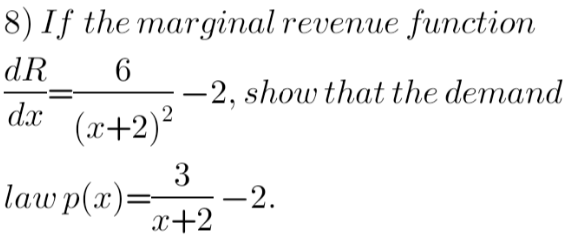
Question Number 113418 Answers: 3 Comments: 1

∫ ((3x−2)/( (√(x^2 +2x+26)))) dx

$$\:\int\:\frac{\mathrm{3x}−\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}}\:\mathrm{dx} \\ $$

Question Number 113323 Answers: 2 Comments: 0

Question Number 113275 Answers: 2 Comments: 0

∫ (dx/(3sin x+sin^3 x)) ?

$$\:\int\:\frac{\mathrm{dx}}{\mathrm{3sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}\:? \\ $$

Question Number 113218 Answers: 1 Comments: 0

Question Number 113203 Answers: 1 Comments: 0

calculate ∫_0 ^∞ (dx/(x^4 +2x^2 +3))

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}} \\ $$

Question Number 113198 Answers: 1 Comments: 0

.... calculus.... Evaluate ::: I :=∫_0 ^( 1) (1/( (√(x(x+1)(x+2)(x+3)+1))−3x))dx=??? M.N.july 1970#

$$\:\:\:\:\:\:\:\:\:....\:{calculus}.... \\ $$$$\:\:\:\:\:\:\mathscr{E}{valuate}\:::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{I}\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)+\mathrm{1}}−\mathrm{3}{x}}{dx}=??? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$$$\:\: \\ $$

Question Number 113159 Answers: 2 Comments: 0

∫_0 ^1 x^2 log(1−x)dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {log}\left(\mathrm{1}−{x}\right){dx} \\ $$

Question Number 113111 Answers: 1 Comments: 0

find the area bounded by the curve y^2 =x^3 and the lines x=0 y=1 and y=2

$${find}\:{the}\:{area}\:{bounded}\:{by}\:{the}\:{curve}\:{y}^{\mathrm{2}} ={x}^{\mathrm{3}} \:{and}\:{the}\:{lines}\:{x}=\mathrm{0}\:{y}=\mathrm{1}\:{and}\:{y}=\mathrm{2} \\ $$

Question Number 113110 Answers: 2 Comments: 2

∫_0 ^1 (√(x(x−1)dx))

$$\overset{\mathrm{1}} {\int}_{\mathrm{0}} \sqrt{{x}\left({x}−\mathrm{1}\right){dx}} \\ $$

Question Number 113004 Answers: 2 Comments: 0

prove that _0 ∫^( ∞) cos(x^2 )dx = _0 ∫^( ∞) sin(x^2 )dx =((√π)/(2(√2)))

$${prove}\:{that} \\ $$$$\:_{\mathrm{0}} \int^{\:\infty} \:{cos}\left({x}^{\mathrm{2}} \right){dx}\:=\:\:_{\mathrm{0}} \int^{\:\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Question Number 112997 Answers: 1 Comments: 3

∫(( tan x dx)/( (√(sec^3 x + 1)))) = ?

$$\int\frac{\:{tan}\:{x}\:{dx}}{\:\sqrt{{sec}^{\mathrm{3}} \:{x}\:+\:\mathrm{1}}}\:=\:? \\ $$

Question Number 112958 Answers: 0 Comments: 3

Question Number 112854 Answers: 0 Comments: 3

.... mathematical analysis.... please solve:: Ω =∫_(0 ) ^( ∞) ((x^(4/5) −x^(2/3) )/((1+x^2 )ln(x))) dx =??? ... m.n.july 1970...#

$$\:\:\:\:\:\:\:\:\:....\:{mathematical}\:\:{analysis}....\:\: \\ $$$$ \\ $$$$\:\:\:\:{please}\:\:{solve}:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\Omega\:=\int_{\mathrm{0}\:} ^{\:\infty} \frac{{x}^{\frac{\mathrm{4}}{\mathrm{5}}} \:−{x}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right){ln}\left({x}\right)}\:{dx}\:=??? \\ $$$$ \\ $$$$\:\:...\:{m}.{n}.{july}\:\mathrm{1970}...#\: \\ $$$$ \\ $$$$ \\ $$

Question Number 112847 Answers: 1 Comments: 0

∫ ((x−sin x)/(1−cos x)) dx ?

$$\:\int\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:? \\ $$

Question Number 112792 Answers: 0 Comments: 0

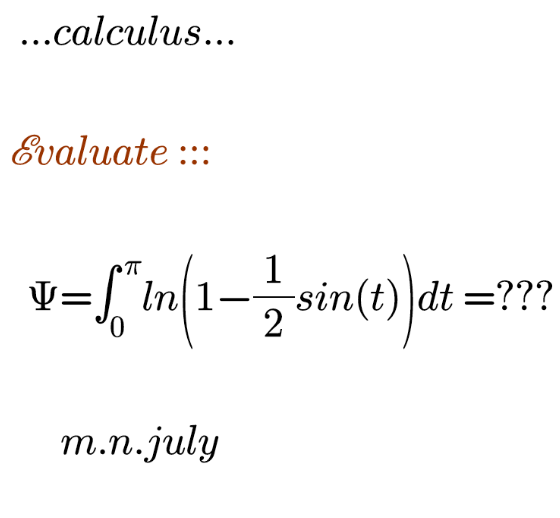
Question Number 112797 Answers: 2 Comments: 0

....calculus... evaluate i: ∫_0 ^( (π/2)) x(√( tan(x))) dx= ??? ii:∫_0 ^( ∞) ((ln(x))/(1+x^2 +x^4 ))dx =??? m.n.july 1970

$$\:\:\:\:\:\:\:\:\:....{calculus}... \\ $$$$\:\:\:{evaluate} \\ $$$$ \\ $$$${i}:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {x}\sqrt{\:{tan}\left({x}\right)}\:{dx}=\:???\: \\ $$$${ii}:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}\:=???\: \\ $$$$\:\:\:{m}.{n}.{july}\:\mathrm{1970} \\ $$

Question Number 112666 Answers: 2 Comments: 0

∫ tan^(−1) ((√((1−x)/(x+1)))) dx ?

$$\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{x}+\mathrm{1}}}\right)\:\mathrm{dx}\:? \\ $$

Question Number 112699 Answers: 3 Comments: 1

(1) ∫ ((sin x e^(√(cos x)) )/( (√(cos x)))) dx (2) ((1+(√(1+sin 2A)))/(1−(√(1+sin 2A))))?? (3)∫ (dx/((x+b)(x^2 +a^2 )))

$$\:\left(\mathrm{1}\right)\:\int\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{e}^{\sqrt{\mathrm{cos}\:\mathrm{x}}} }{\:\sqrt{\mathrm{cos}\:\mathrm{x}}}\:\mathrm{dx}\: \\ $$$$\:\left(\mathrm{2}\right)\:\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2A}}}{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2A}}}??\: \\ $$$$\left(\mathrm{3}\right)\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)} \\ $$

Question Number 112613 Answers: 1 Comments: 2

....number theory... Question : If a , b , c ∈ N ; then prove ::: a!∗b!∗c!∣(a+b+c)! m.n . july 970#

$$\:\:\:\:\:....{number}\:{theory}... \\ $$$$\:\:\:\:\:\:\:{Question}\::\:\:\:\:\:\:\mathrm{I}{f}\:\:\:{a}\:,\:{b}\:,\:{c}\:\:\in\:\mathbb{N}\:\:\:;\:{then}\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}!\ast{b}!\ast{c}!\mid\left({a}+{b}+{c}\right)!\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}\:.\:{july}\:\mathrm{970}# \\ $$

Question Number 112579 Answers: 4 Comments: 0

.... calculus .... Please Evaluate ::: Ω = ∫_0 ^(π/2) ((x/(sin(x))))^2 dx =??? M.N.july 1970#

$$\:\:\:\:\:\:\:\:....\:{calculus}\:.... \\ $$$$\mathscr{P}{lease}\:\:\mathscr{E}{valuate}\:::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{x}}{{sin}\left({x}\right)}\right)^{\mathrm{2}} {dx}\:=???\:\:\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$$$\: \\ $$

Question Number 112520 Answers: 0 Comments: 0

∫(((cos(x)))^(1/3) /(cos(x)))dx

$$\int\frac{\sqrt[{\mathrm{3}}]{{cos}\left({x}\right)}}{{cos}\left({x}\right)}{dx} \\ $$

Question Number 112498 Answers: 0 Comments: 0

∫((ln(1+x)dx)/((1+x^2 )))

$$\int\frac{{ln}\left(\mathrm{1}+{x}\right){dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$

Question Number 112481 Answers: 1 Comments: 0

∫ ((sin 2x)/( (√(1+cos^2 x)))) dx

$$\:\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}}\:\mathrm{dx}\: \\ $$

Question Number 112447 Answers: 0 Comments: 0

calculate ∫_0 ^1 ((ln(1+x^2 ))/(1+x^3 )) dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\:\mathrm{dx} \\ $$

Question Number 112446 Answers: 2 Comments: 0

find ∫_0 ^1 ((ln(1+x^2 ))/(1+x))dx

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$

Pg 142 Pg 143 Pg 144 Pg 145 Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151

Contact: info@tinkutara.com