
IntegrationQuestion and Answers: Page 134
Question Number 121712 Answers: 1 Comments: 0
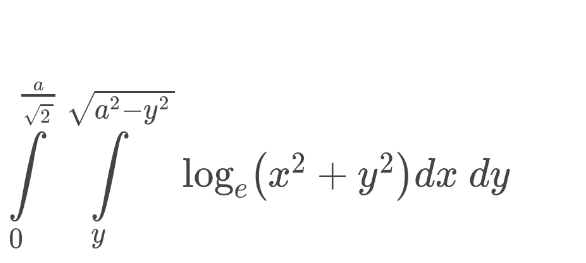
Question Number 121707 Answers: 1 Comments: 0
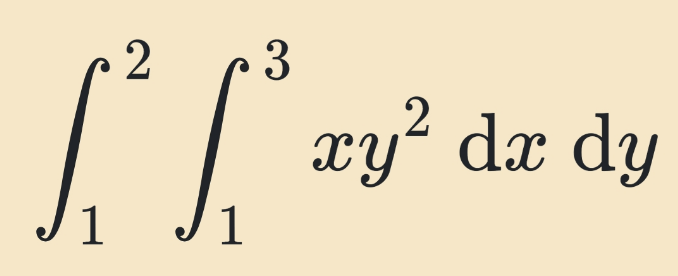
Question Number 121704 Answers: 1 Comments: 0
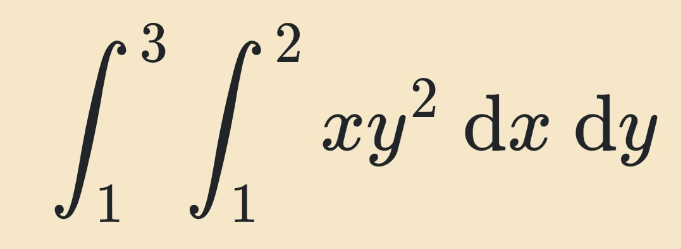
Question Number 121696 Answers: 2 Comments: 0
Question Number 121680 Answers: 1 Comments: 0
Question Number 121674 Answers: 3 Comments: 0
Question Number 121611 Answers: 1 Comments: 2
Question Number 121602 Answers: 2 Comments: 0

Question Number 121601 Answers: 4 Comments: 0
$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{x}\:\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }}\:? \\ $$
Question Number 121548 Answers: 1 Comments: 0
Question Number 121519 Answers: 1 Comments: 0
Question Number 121498 Answers: 1 Comments: 0
Question Number 121500 Answers: 3 Comments: 1
Question Number 121492 Answers: 3 Comments: 0
Question Number 121480 Answers: 0 Comments: 0
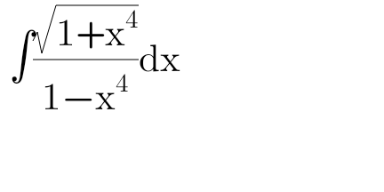
Question Number 121466 Answers: 1 Comments: 2
Question Number 121397 Answers: 2 Comments: 0
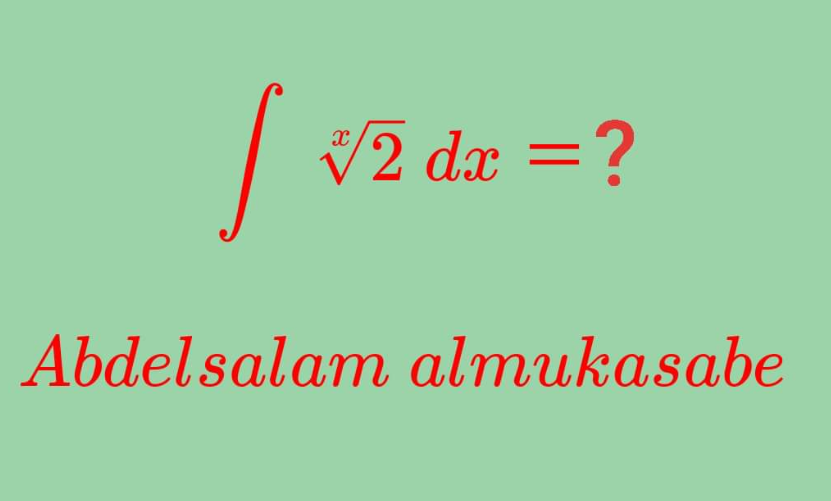
Question Number 121384 Answers: 2 Comments: 2
$$\:\int\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx}\: \\ $$
Question Number 121315 Answers: 2 Comments: 0
Question Number 121314 Answers: 1 Comments: 0
Question Number 121300 Answers: 2 Comments: 1
Question Number 121225 Answers: 2 Comments: 0
Question Number 121224 Answers: 1 Comments: 0
Question Number 121203 Answers: 2 Comments: 0
Question Number 121174 Answers: 4 Comments: 0
Question Number 121119 Answers: 4 Comments: 0
Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 Pg 134 Pg 135 Pg 136 Pg 137 Pg 138
