
IntegrationQuestion and Answers: Page 132
Question Number 122626 Answers: 2 Comments: 0
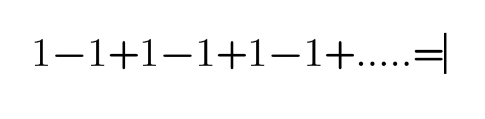
Question Number 122625 Answers: 0 Comments: 0
Question Number 122614 Answers: 4 Comments: 0

Question Number 122588 Answers: 2 Comments: 0
Question Number 122587 Answers: 5 Comments: 0
Question Number 122572 Answers: 1 Comments: 0
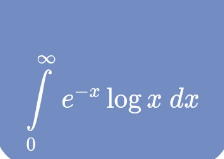
Question Number 122544 Answers: 0 Comments: 0
$$\:{any}\:{one}\:{can}\:{explain}\:{me}\:{about} \\ $$$${Fresnel}\:{integral}\:? \\ $$
Question Number 122542 Answers: 1 Comments: 0
Question Number 122528 Answers: 1 Comments: 0
Question Number 122506 Answers: 1 Comments: 0

Question Number 122496 Answers: 2 Comments: 0
Question Number 122469 Answers: 1 Comments: 5

Question Number 122461 Answers: 2 Comments: 2
Question Number 122432 Answers: 0 Comments: 0

Question Number 122430 Answers: 1 Comments: 0
Question Number 122397 Answers: 4 Comments: 0
Question Number 122366 Answers: 1 Comments: 0

Question Number 122349 Answers: 1 Comments: 1
Question Number 122330 Answers: 2 Comments: 0
Question Number 122323 Answers: 1 Comments: 1
Question Number 122298 Answers: 1 Comments: 0
Question Number 122290 Answers: 1 Comments: 1
Question Number 122274 Answers: 2 Comments: 0
$$\:\:\:\int\:\frac{\sqrt{\mathrm{1}−\sqrt{{x}}}}{\:\sqrt{\mathrm{1}+\sqrt{{x}}}}\:{dx}\:?\: \\ $$
Question Number 122205 Answers: 1 Comments: 2
Question Number 122186 Answers: 2 Comments: 0
Question Number 122160 Answers: 1 Comments: 0

Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 Pg 134 Pg 135 Pg 136
