Question and Answers Forum

IntegrationQuestion and Answers: Page 131

Question Number 122934 Answers: 0 Comments: 1

Question Number 122927 Answers: 1 Comments: 1

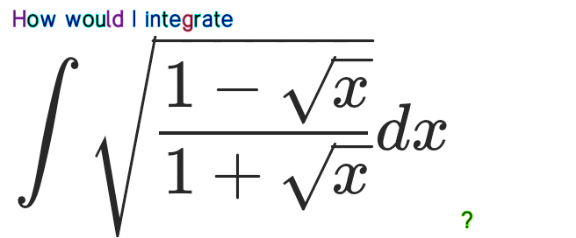
Question Number 122922 Answers: 1 Comments: 0

∫_0 ^(π/4) ((cos x+sin x)/(16sin 2x+9)) dx

$$\:\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{16sin}\:\mathrm{2}{x}+\mathrm{9}}\:{dx}\: \\ $$

Question Number 122919 Answers: 2 Comments: 0

Question Number 122885 Answers: 3 Comments: 1

Question Number 122884 Answers: 1 Comments: 1

Question Number 122882 Answers: 1 Comments: 0

... nice calculus... prove that ::: Ω=∫_0 ^( 1) (((x^ϕ −1)/(ln(x))))^2 dx=(√5) ln(ϕ) .m.n.

$$\:\:\:\:\:\:\:\:\:...\:\:{nice}\:\:{calculus}... \\ $$$$\:\:\:\:{prove}\:{that}\:::: \\ $$$$\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{x}^{\varphi} −\mathrm{1}}{{ln}\left({x}\right)}\right)^{\mathrm{2}} {dx}=\sqrt{\mathrm{5}}\:{ln}\left(\varphi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$

Question Number 122877 Answers: 1 Comments: 1

∫ (sin^(−1) (x))^2 dx ?

$$\:\:\int\:\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} \:{dx}\:? \\ $$

Question Number 122875 Answers: 1 Comments: 0

∫(((x^2 +1)dx)/(x^4 +x^2 +1)) = ...

$$\:\int\frac{\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}\right)\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:=\:... \\ $$$$\: \\ $$

Question Number 122867 Answers: 2 Comments: 0

Question Number 122853 Answers: 0 Comments: 2

Question Number 122838 Answers: 1 Comments: 0

∫ (dx/( (((x−1)^3 (x+2)^5 ))^(1/4) )) ?

$$\:\:\int\:\frac{{dx}}{\:\sqrt[{\mathrm{4}}]{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }}\:? \\ $$

Question Number 122828 Answers: 1 Comments: 0

Question Number 122823 Answers: 1 Comments: 0

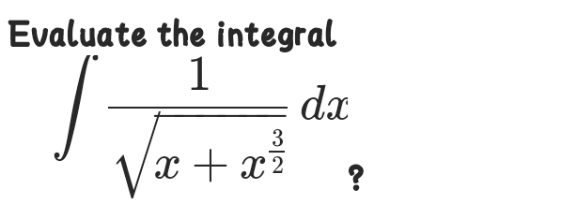
Question Number 122822 Answers: 1 Comments: 0

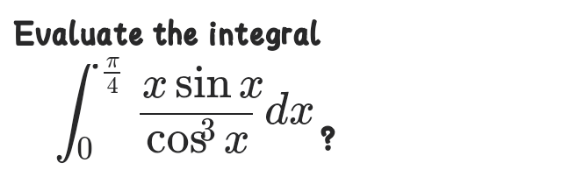
Question Number 122807 Answers: 1 Comments: 1

Question Number 122751 Answers: 3 Comments: 0

∫_0 ^(1/(√2)) ((x sin^(−1) (x^2 ))/( (√(1−x^4 )))) dx ?

$$\:\underset{\mathrm{0}} {\overset{\mathrm{1}/\sqrt{\mathrm{2}}} {\int}}\:\frac{{x}\:\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:{dx}\:?\: \\ $$

Question Number 122748 Answers: 3 Comments: 0

∫_0 ^3 (dx/((3−x)(√(x^2 +1)))) ?

$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{{dx}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:? \\ $$

Question Number 122734 Answers: 1 Comments: 0

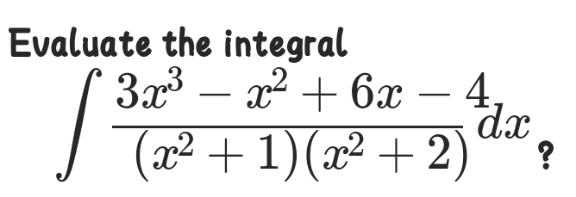
Question Number 122713 Answers: 0 Comments: 0

... advanced math ... two simple and nice integrals: prove that:: Ω_1 =∫_0 ^( ∞) ((sin(e^(−γ) x)ln(x))/x) dx=0 Ω_2 =∫_0 ^( ∞) ((sin(x^((√2)/2) )ln(x))/x)dx=−πγ note :: γ : Euler−mascheroni constant. .m.n.

Question Number 122697 Answers: 3 Comments: 0

∫ (dx/( (√((x−a)(b−x))))) ?

$$\:\:\int\:\frac{{dx}}{\:\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}}\:? \\ $$

Question Number 122689 Answers: 1 Comments: 0

Evaluate the integral ∫ (((x)^(1/3) +1)/( (x)^(1/3) −1)) dx

$$\:{Evaluate}\:{the}\:{integral}\: \\ $$$$\:\:\int\:\frac{\sqrt[{\mathrm{3}}]{{x}}\:+\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{x}}\:−\mathrm{1}}\:{dx}\: \\ $$

Question Number 122671 Answers: 1 Comments: 2

...nice integral... prove that :: ∫_0 ^( ∞) cos(πnx)((1/x^2 )−((πcoth(πx))/x))dx =^(???) πln(1−e^(−πn) ) .m.n.

$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{integral}... \\ $$$$\:\:\:{prove}\:{that}\:\::: \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} {cos}\left(\pi{nx}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\pi{coth}\left(\pi{x}\right)}{{x}}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{???} {=}\pi{ln}\left(\mathrm{1}−{e}^{−\pi{n}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$

Question Number 122636 Answers: 1 Comments: 0

...nice calculus... In AB^Δ C prove :: ∗: sin((A/2))sin((B/2))sin((C/2))≤(1/8) ......................... ∗∗:: max(cos((A/2))cos((B/2))cos((C/2)))=?

$$\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:{In}\:\:\mathrm{A}\overset{\Delta} {\mathrm{B}C}\:\:{prove}\:::\: \\ $$$$\:\:\:\ast:\:\:{sin}\left(\frac{\mathrm{A}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{B}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{C}}{\mathrm{2}}\right)\leqslant\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$......................... \\ $$$$\:\:\:\:\ast\ast::\:\:\:{max}\left({cos}\left(\frac{\mathrm{A}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{B}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{C}}{\mathrm{2}}\right)\right)=? \\ $$$$\:\:\:\:\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\: \\ $$

Question Number 122631 Answers: 2 Comments: 2

solve ∫_((a−1)^2 ) ^a^2 cosh^(−1) (1/( (√(a−(√x))))) dx with a>0

$$\mathrm{solve}\:\underset{\left({a}−\mathrm{1}\right)^{\mathrm{2}} } {\overset{{a}^{\mathrm{2}} } {\int}}\mathrm{cosh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{{a}−\sqrt{{x}}}}\:{dx}\:\mathrm{with}\:{a}>\mathrm{0} \\ $$

Question Number 122626 Answers: 2 Comments: 0

Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 Pg 134 Pg 135

Contact: info@tinkutara.com